カイ二乗分布とは何か？確率密度関数、期待値、分散、カイ二乗検定。

Tweet

【目次】

カイ二乗分布の定義と例
カイ二乗分布のグラフ
カイ二乗分布の確率密度関数、期待値、分散
カイ二乗分布を使った検定
練習問題
練習問題回答

カイ二乗分布の定義と例

カイ二乗分布（分布,Chi-squred distribution）とは、独立性検定などの統計学的検定によく利用される分布で、(自由度が極端に大きくならない限り)右に歪んだ分布です。

カイ二乗分布の定義は以下のようになります。

カイ二乗分布の定義

確率変数Z₁,Z₂,・・・,Z_nが独立で、それぞれに標準正規分布に従うとき、Xを

とすると、Xは自由度nのカイ二乗分布に従う。またXが自由度nのカイ二乗分布に従うことを

と表す。

早速、例を見てみましょう。

確率変数Z₁,Z₂,Z₃,Z₄が独立で、それぞれ標準正規分布に従うとします。確率変数Xを

と定義すると、Xは自由度4のカイ二乗分布に従います。

これが成り立つことをシュミレーションで確かめて見ましょう。

まず、それぞれ独立のZ₁,Z₂,Z₃,Z₄を標準正規分布からRを利用してランダムに抽出して見ます。

なお以下のコードで標準正規分布に従うZ₁,Z₂,Z₃,Z₄を１つづつ抽出することができます。

# Z1,Z2,Z3,Z4をそれぞれ標準正規分布から抽出する。
Z1=rnorm(1,0,1)
Z2=rnorm(1,0,1)
Z3=rnorm(1,0,1)
Z4=rnorm(1,0,1)

まず１回目は以下の数値が抽出されました。(以下の結果は、実際にはround()関数を利用し、少数第３位までで四捨五入してあります。)

 
それでは最初のXを計算してみます。

=
=

これを何度も繰り返し、Xがどのような分布を描くか見てみます。

ここでは、3000回繰り返して、以下のように、X₁,・・・X₃₀₀₀のヒストグラムを作成しました。

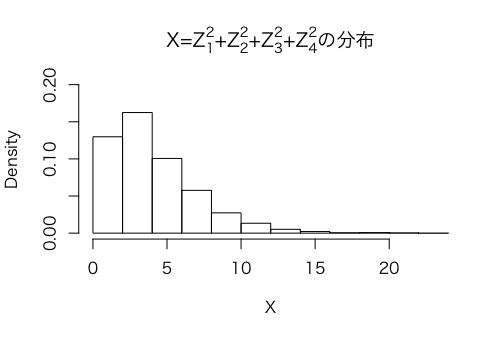
これに自由度4のカイ二乗分布の確率密度関数のグラフを重ねてみます。

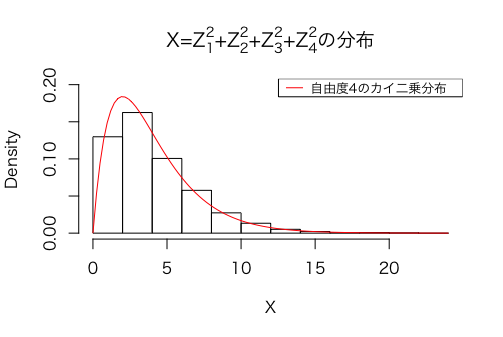
Xが自由度４のカイ二乗分布に従っていることが確認できますね。

カイ二乗分布のグラフ

以下のように、カイ二乗分布は自由度が大きくなるほど、より大きな値をとる確率が増えていく右に歪んだ分布です。

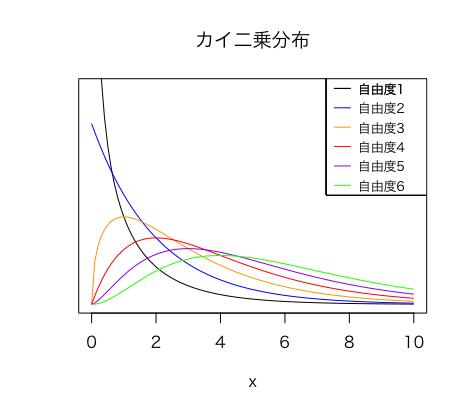
またカイ二乗分布は、自由度が無限大に近くに連れて、正規分布に近づきます。

以下に、自由度30、自由度100のカイ二乗分布のグラフを紹介します。

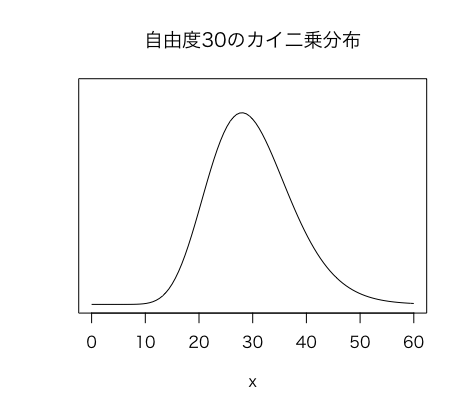
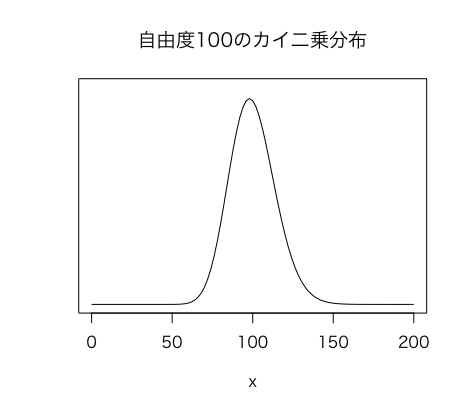
以上のように、自由度30ではまだ、やや右に歪んでいますが、自由度100のカイ二乗分布になると、ほぼ正規分布に見えますね。

カイ二乗分布の確率密度関数、期待値、分散

カイ二乗分布の確率密度関数、期待値E(X)、分散Var(X)

確率変数Xが自由度pのカイ二乗分布に従うとき、つまり

のとき、

・確率密度関数　
　

※自由度
※ここではガンマ関数と呼ばれ、nが自然数のとき、となります。

・期待値
E(X)=p

・分散
Var(X)=2p

カイ二乗分布を使った検定

カイ二乗分布は、適合度検定や独立性検定など、検定統計量がカイ二乗分布に従う検定に利用されます。詳しくは「統計学の基礎」の「２変数の独立性の検定（カイ二乗検定）」の中でまとめていこうと思います。

練習問題

Z₁,Z₂,Z₃がそれぞれ独立して標準正規分布に従うとし、確率変数Xを以下のように定義すると、Xはどんな分布に従うか？またXの期待値と分散を求めよ。

練習問題回答

・Xは自由度３のカイ二乗分布に従う。
・期待値: E(X)=3
・分散: Var(X)=6

Tweet