社会人が統計学の基礎を学び、実務で活かす

MENU

t分布とは何か？

HOME »
確率分布 »
t分布とは何か？

【目次】

t分布の定義と標準正規分布との関係
t分布の確率密度関数、期待値、分散
t分布を使った検定

t分布とは何か？標準正規分布との関係

t分布（ティー分布、t-distribution）とは、統計学的検定（t検定、相関関係の検定、線形回帰の検定など）によく利用される分布で、分布の形は標準正規分布によく似ています。

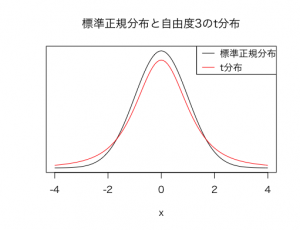
t分布は、標準正規分布に非常によく似ているのですが、
標準正規分布に比べて、t分布の方が少しだけ、

•ベル型の頂点の位置が低く、
•左右に広がる裾が厚い。

という特徴があります。

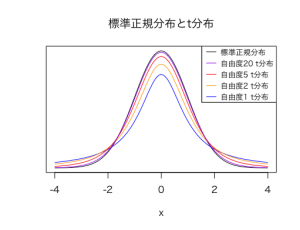
t分布は、自由度（じゆうど）と呼ばれるパラメータを持ち、自由度が大きくなるほど、

•ベル型の頂点の位置が高くなっていき、
•左右に広がる裾が薄くなっていきます。

そして、自由度が大きくなるにつれ、標準正規分布に近づいていきます。

つまり、t分布の自由度が十分に大きくなると、標準正規分布に収束します。

よく使われる基準としては、自由度が30以上のt分布は標準正規分布と同じとみなしてほぼ問題がない、というものがあります。

t分布の定義は以下のようになります。

t分布の定義
n個の確率変数 $X_1,X_2,\cdots,X_n$ がすべて独立で、同じ正規分布 $N(\mu,\sigma^2)$ に従う時、

この確率変数 $X_1,X_2,\cdots,X_n$ の平均を $\bar{X}=\displaystyle{\frac{\Sigma_{i=1}^{n} X_i}{n}}$ 、分散を $S^2=\displaystyle{\frac{\Sigma_{i=1}^{n}(X_{i}-\bar{X})^2}{n-1}}$ とし、
確率変数Tを $T=\displaystyle{\frac{\bar{X}-\mu}{S/\sqrt{n}}}$ と定義すると、
この確率変数Tは自由度 $n-1$ のt分布に従う。

※標本分散 $S^2$ に関しては「統計学の基礎」で詳しく解説します。

確率変数Tが自由度n-1のt分布に従うことを以下のように表記します。

$T\sim t_{n-1}$

例

日本人の成人男性の身長が平均値&mu=171、分散σ²=64、つまり標準偏差σ=8の正規分布に従うと仮定します。

つまり、日本人の成人男性をランダムに抽出したとき、その人の身長を確率変数をXとすると、

$X\sim N(171,64)$

とします。

さて、この確率分布から3人を抽出し、それぞれの身長を $X_1,X_2,X_3$ としましょう。

上記の定義のように $\bar{X}$ と $S^2$ を求めるには

• $\bar{X}=(X_1+X_2+X_3)/3$

• $S^2=\displaystyle{\frac{(X_1-\bar{X})^2+(X_2-\bar{X})^2+(X_3-\bar{X})^2}{2}}$

つまり、
• $S=\displaystyle{\sqrt{\frac{(X_1-\bar{X})^2+(X_2-\bar{X})^2+(X_3-\bar{X})^2}{2}}}$

とすると、確率変数 $T=\displaystyle{\frac{\bar{X}-171}{S/\sqrt{3}}}$ は自由度n-1=2のt分布に従います。

実際にシュミレーションしてみます。

以下の手順を1000回繰り返します。

①平均値171、分散64の正規分布から３個の値をランダムに抽出する。
②抽出した３個の値から $\bar{X}$ と $S$ を算出し、それを用いてTを計算する。

これを1000回繰り返し、1000個のT（T₁,T₂,・・・,T₁₀₀₀としましょう。）のヒストグラムを描く。

そしてこのヒストグラムに自由度２のt分布を重ねてみます。

それでは、１回目。

> round(rnorm(3,171,8),digits=2)
[1] 165.99 172.47 164.31

上記のコードで３つの数字を正規分布から発生させました。

$\bar{X}$ と $S$ を計算すると、

$\bar{X}=(165.99+172.47+164.31)/3=167.59$
$S=\displaystyle{\sqrt{\frac{(165.99-167.59)^2+(172.47-167.59)^2+(164.31-167.59)^2}{2}}}=4.30$

上記より $T_1$ の実現値 $t_1$ は

$t_1=\displaystyle{\frac{167.59-171}{4.30/\sqrt{3}}}=-1.37$

ということで１個目のTの実現値 $t_1=-1.37$ となりました。

それでは２回目！

> round(rnorm(3,171,8),digits=2)
[1] 163.82 172.48 183.70

$\bar{X}=173.33$ 、 $S=9.97$ なので、

$t_2=\displaystyle{\frac{173.33-171}{9.97/\sqrt{3}}}=0.41$

２個目のTの実現値は0.41です。

同じように全部でTを1000個求めて、そのヒストグラムを作ります。

以下が、そのヒストグラム。

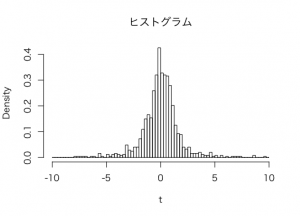
自由度２のt分布を重ねてみると以下のようになりますね。

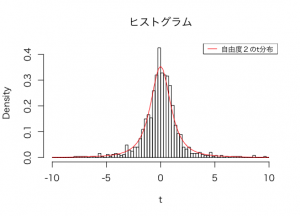
このように確率分布Tは自由度n-1のt分布に従っているのが理解頂けると思います。

t分布の確率密度関数、期待値、分散

t分布の確率密度関数(pdf)、期待値、分散は以下の通りです。

t分布の確率密度関数、期待値E(X)、分散Var(X)

確率変数Xが自由度pのt分布に従う時、つまり、

$X\sim t_p$

のとき、

•確率密度関数
$f_{X}(x)=\displaystyle{\frac{\Gamma({\frac{p+1}{2}})}{\Gamma({\frac{p}{2}})}\frac{1}{\sqrt{p\pi}}\frac{1}{\big(1+(\frac{x^2}{p})\big)^{\frac{(p+1)}{2}}}}$ (-∞<x<∞)

※自由度 $p=1,2,3,\cdots$
※-∞<x<∞とは、xがマイナス無限大からプラス無限大までのすべての実数を取り得る、という意味です。

•期待値
$E(X)=0$

•分散
$Var(X)=\frac{p}{p-2}$

t分布を使った検定

t分布は、母集団の平均値の統計学的検定や、相関係数の検定、回帰分析のパラメータの検定など、頻繁に利用される統計学的検定において、非常に多く利用される分布です。

詳しくは各検定手法について説明したページに譲りますが、簡単に例を挙げたいと思います。

例えば、日本人の正社員の平均年収が400万円以上あるかどうか、を統計学的検定によって結論付けたいとします。

仮に、10人をランダムに抽出して、その10人の平均年収を $\bar{X}$ 、その標本分散を $S^2$ 、また、母集団の本当の平均値を400万円と仮定すると、

確率変数 $T=\displaystyle{\frac{\bar{X}-4,000,000}{S/\sqrt{10}}}$

は自由度9のt分布に従います。この性質を利用して、実際に得られたデータが、本当の平均年収を400万円だったと仮定した時、どれくらい起こる確率があるのか？を求め、検定の結論づけに利用します。

なお、統計学的検定の意味や各手法に関しては「統計学の基礎」のページで基本から解説します。

確率分布

PAGETOP

Copyright © 【統計学の入門サイト】統計ドットリンク All Rights Reserved.

Powered by WordPress & BizVektor Theme by Vektor,Inc. technology.