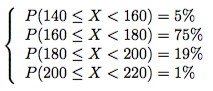連続型確率分布と離散型確率分布
確率変数に連続型と離散型があるように、確率分布にも連続型確率分布と、離散型確率分布があります。
連続型確率分布とは、連続型の確率変数が従う確率分布であり、離散型確率分布とは離散型の確率変数が従う確率分布です。
まずは離散型の確率分布から見ていきましょう。
離散型確率分布
例1: サイコロの目
「確率分布とは何か?」のページで紹介した、サイコロの目の確率分布はまさに離散型確率分布ですね。
歪んでいないサイコロを1回振ったときに出た目を確率変数Xとすると、X={1,2,3,4,5,6}とXが取り得る値を一つずつ列挙することができます。つまりX
は離散型の確率変数です。
そして離散型の確率変数が従う分布は離散型確率分布です。
この例の場合は、確率分布は以下の表の通りです。
確率分布表
| 出る目 | 確率 |
| 1 | 1/6 |
| 2 | 1/6 |
| 3 | 1/6 |
| 4 | 1/6 |
| 5 | 1/6 |
| 6 | 1/6 |
| それ以外 | 0 |
例2: 何回サイコロを振ると1の目が出るか?
「連続型確率変数と離散型確率変数の違いとは?」のページで紹介した、何回サイコロを振ると1の目が出るかの分布について考えてみましょう。
まず、サイコロを1の目が出るまで振り続けた時、サイコロを振った回数を確率変数Xとします。Xの取り得る値は{1,2,3,4,5,・・・}と列挙することができるのでXは離散型の確率変数でしたね。
離散型の確率変数は必ずしも有限ではなく、このXのように1以上のすべての整数の値を取り得るため上限がなく、Xが取り得る値は無限大個になることもある、というのは前回のページで学習しました。
さて、Xは離散型の確率変数なので、このXが従う分布は離散型確率分布です。
X=1の確率は、1回目からいきなり1の目が出る確率なので、1/6(約1.666)ですね。
つまり
ということです。
2回目で初めて1が出る確率はどうでしょうか?
まず、1回目で1が出ない、つまり1以外の目が出て、2回目で1が出る確率ということですね。
1回目で1以外が出る確率は5/6ですね。
そして、2回目で1が出る確率は1/6です。
つまり2回目で初めて1が出る(X=2)の確率は
ということになります。
数式を使うと
ということです。
さて、3回目で初めて1が出る確率は、つまりX=3の確率はどうでしょうか?
1回目で1以外が出る確率は5/6、2回目も1以外が出る確率は5/6、3回目に1が出る確率は1/6なので、3回目で初めて1が出る(X=3)確率は
つまり
となります。
同じようにX=4, X=5, X=6 ・・・と続けていくと、それぞれの確率は以下のようになります。
確率分布表で表すと以下のようになりますね。
確率分布表
| X(回数) | 確率 |
| 1 | 0.1666 |
| 2 | 0.1388 |
| 3 | 0.1157 |
| 4 | 0.0964 |
| 5 | 0.0803 |
| 6 | 0.0669 |
| ・・・ | ・・・ |
次に連続型の確率分布を見てみましょう。
連続型確率分布
連続型確率分布は連続型の確率変数が従う確率分布です。
これも前回のページ「連続型確率変数と離散型確率変数の違いとは?」で紹介した連続型の確率変数である、人間の身長の例で考えてみましょう。
例:人間の身長
離散型の確率変数は、例えば上記のサイコロの例のように
や
などと、確率変数が取り得る値を一つづつ列挙して、その確率を表現することができました。
しかし、連続型の確率変数は値を一つ一つ列挙することができません。
例えば、日本人の成人男性をランダムに一人選んだとき、その人の身長を確率変数Xとすると、丁度ぴったり175.00000・・・cmの人というのは理論的にはいないため、
ということになってしまいます。
175cmに限らず同じ理由で176cmも180cmも丁度その身長の人が選ばれる確率は0です。
それではどのように確率分布を表現するかというと、170cm以上180cm未満のように区間を区切って分布を表現します。
確率分布表を作ると以下のような感じになります。
確率分布表
| X(身長) | 確率 |
| 140cm以上150cm未満 | 1% |
| 150cm以上160cm未満 | 4% |
| 160cm以上170cm未満 | 30% |
| 170cm以上180cm未満 | 45% |
| 180cm以上190cm未満 | 15% |
| 190cm以上200cm未満 | 4% |
| 200cm以上210cm未満 | 1% |
なお、筆者は正確な日本人の身長の分布を知らないので、上記の例は分かりやすく単純化しています。
また、区切りは10cmごとである必要はありません。連続型の確率分布表を作るときは分かりやすい、または、利用しやすい区切り幅で作りましょう。
数式で確率分布を表現するときも以下のように区間ごとに表現します。
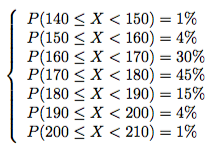
以上で連続型確率分布と離散型確率分布の違いを理解していただけたと思います。仕事や生活の中でデータを分析する際、離散型も連続型も両方の変数が頻繁に登場するので、違いを理解して分析に役立てることができるのが重要です。
また、確率変数やデータの分布を見て、理解するためにはヒストグラムというグラフを作成し、可視化するのが基本です。ヒストグラムについては「データの要約、作図、グラフ化」のページで解説していきます。
練習問題
上述の日本人の成人男性の身長の分布の区切りを少し大きくして、20cm毎、140-160cm, 160-180cm, 180-200cm, 200-220cm の目盛り確率分布表と数式での確率分布表を書き換えてみてください。
練習問題回答
確率分布表
| X(身長) | 確率 |
| 140cm以上160未満 | 5% |
| 160cm以上180cm未満 | 75% |
| 180cm以上200cm未満 | 19% |
| 200cm以上220cm未満 | 1% |