連続型確率変数と離散型確率変数
確率変数には連続型確率変数(Continuous Random Variable)と、離散型確率変数(Discrete Random Variable)の2種類があります。細かく言うと連続型と離散型の混合変数(Mixed Random Variable)もありますが、基礎を固めるためには二つを知っておけば十分です。
連続型確率変数とは、連続の値をとる確率変数のことで、離散型確率変数とは、不連続の値をとる確率変数のことです。
それぞれ見ていきましょう。
連続型確率変数
連続型確率変数は、長さ、重さ、時間、何らかしらの物質の量や体積、などなど定められた範囲で連続した数値をとる確率変数です。
例を挙げます。
例1:人間の身長
日本人の成人男性をランダム一人選んだ時、その選ばれた人の身長を確率変数X
とします。例えば日本一背が低い成人男性の身長を140cm、高い人の身長を220cmと仮定すると、Xは140から220の値をとりますね。
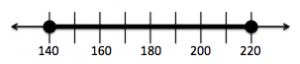
そして、このXは140から220の間で連続の値をとります。
連続の値、というのはどう言うことかというと、140から220の間のすべての実数の値とる可能性があるということです。
実数は数直線上をぎっしりと埋め尽くしていますから、厳密にいうと、ある人と全く同じ身長の人はいません。
例えば、筆者の身長は175.5cmなのですが、厳密にいうと丁度ぴったり175.5cm(つまり175.50000000000000・・・cm)というのはあり得ないのです。
連続型の変数では、どんなに細かく目盛りを区切ったとしても175.50cmと175.51cmの間に例えば175.503などの実数が存在するため、変数が取り得るすべての値を列挙することは不可能です。
このように、連続型の確率変数では、同じ値が二つ得られる確率は厳密には0です。
それだけではなく、ある値が得られる確率も0であると考えます。
つまり P(X=175.5)=0 ということです。
なぜならば、Xが175.5ぴったりという値になることはあり得ないからです。
例2:100メートル走のタイム
100メートル走のタイムをXとすると、理論的にはXは0より大きい実数を取り得る連続型の確率変数です。
現在、技術的に可能なストップウォッチでは0.0001秒単位なのか0.00001秒単位なのか、どこまで細かく目盛りを設定できるのかはわかりませんが、理論上はどんなに目盛りを細かく設定しても、必ずその間にもっと細かい目盛りの数字があります。
もちろん、100メートル走のタイムに限らず、時間の長さを測定するときは理論上は連続型の変数になります。
(物理学的な難しい話にはここでは深入りしません。)
離散型確率変数
離散型確率変数とは取り得る値を一つ一つ列挙できる確率変数のことです。ただし、取り得る値が無限大個あるケースもあるので、すべての値を列挙できるとは限りません。
サイコロを振って出る目は離散型確率変数の代表的なものですね。
例1:サイコロの目
何度も登場している例ですが、改めてサイコロを1回振って出る目をXとすると、Xは{1,2,3,4,5,6}の値を取り得る離散型の確率変数ですね。{1,2,3,4,5,6}のように、Xが取り得る値をすべて列挙することができます。
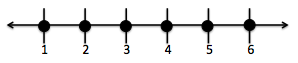
例2:何回サイコロを振ると1の目がでるか?
1の目が出るまで何度もサイコロを振り続ける試行を行い、サイコロを振った回数をXとします。
例えば1回目からいきなり1が出た場合、Xの実現値は1、つまりx=1ですね。
サイコロを10回振ってやっと1が出た時、x=10となります。
Xの取り得る値を列挙してみると、X={1,2,3,4,5,6,7,8,9,10,11,12,・・・}となり、一つ一つ列挙していくことができるので、Xは離散型の確率変数であることが分かります。
ただし、この確率変数には取り得る値の上限がありません。
非常に低い確率ですが、1億回サイコロを振っても1がでない確率も0ではないのです。
これは取り得る値が無限大個ある、すべての値を列挙することができない離散型確率変数のよい例ですね。
練習問題
すべての日本の成人から一人をランダムに選んだ時、その人の年収を確率変数Xとします。Xは離散型か?それとも連続型の確率変数か?
練習問題回答
年収は1円単位で区切ることができるので、厳密にいうとXは離散型の確率変数です。仮に日本最高年収を200億円とすると、
X={0,1,2,3,4,5,6,・・・,19999999999, 20000000000}
と、すべての値を列挙することができます。
ただし、実際の統計解析で年収を扱うときは、通常は連続型の変数として扱います。

