確率変数の期待値
確率変数の期待値(Expected value)とは、ある試行を永遠に繰り返した時に得られる実現値の平均のことです。
例えば、歪んでいないサイコロを１回振って出る目を確率変数Xとします。Xの取り得る範囲はX={1,2,3,4,5,6}ですね。
このサイコロを10回振って実現値が{1,4,2,4,1,1,6,3,2,5}と出たとします。この時の平均値は
となりますね。
このケースではサイコロを10回しか振っていませんが、これを、20回、30回、100回、1000回、10000回・・・、とサイコロを永遠に降り続けると、その平均値は3.5に近づいていきます。つまり、この確率変数Xの期待値は3.5ということです。
また、確率変数Xの期待値のことをE(X)と表します。
このEは期待値は英語でExpected value といいますので、その頭文字です。
別の言い方をすると、期待値とは確率変数の各実現値に割り当てられた確率で重みをつけた加重平均のことです。
この確率変数Xの分布は以下の図のようになりますので、
確率分布表
| 出る目 | 確率 |
| 1 | 1/6 |
| 2 | 1/6 |
| 3 | 1/6 |
| 4 | 1/6 |
| 5 | 1/6 |
| 6 | 1/6 |
| それ以外 | 0 |
この確率変数Xの実現値x=1, x=2, x=3, x=4, x=5, x=6をそれぞれ割り当てられた確率で加重平均をとると、
となります。
期待値の数学的定義
ここまでは、直感的に期待値を理解できる言葉で解説してきましたが、これを数学的に定義すると以下のようになります。
•離散型確率変数の期待値
離散型確率変数Xの各実現値を
•連続型確率変数の期待値
連続型確率変数Xは各実現値をひとつひとつ列挙することができないので、
となります。
離散型確率変数の期待値の例
それでは、上記の定義を使って離散型確率変数の期待値を考えてみましょう。先ほどのサイコロを少し改造して、５の目を１に、６の目を２に書き換えてみます。そうすると、１の目と２の目が出る確率が２倍になり、５の目と６の目が出る確率が０になりますので、確率分布は以下のように変わります。
確率分布表
| 出る目 | 確率 |
| 1 | 1/3 |
| 2 | 1/3 |
| 3 | 1/6 |
| 4 | 1/6 |
| それ以外 | 0 |
このサイコロを振ったときに出る目Xの期待値を求めてみると、
となり、この期待値E(X)は2.7であることが分かります。
それでは次に連続型確率変数の期待値の例を見てみましょう。
連続型確率変数の期待値の例
連続型確率変数の期待値を求めるには、その確率密度関数を使います。
それでは、確率密度関数、確率質量関数とは何か？のページで学習した、日本人の成人男性の身長の分布を近似的にベル型の分布で表した確率密度関数を使って、日本人男性の身長の期待値を求めてみましょう。
日本人男性の身長の平均を171cmと仮定したこの分布の確率密度関数は以下で表すことが出来るのでしたね。
そして身長の分布をグラフで表すと以下のようになりますね。
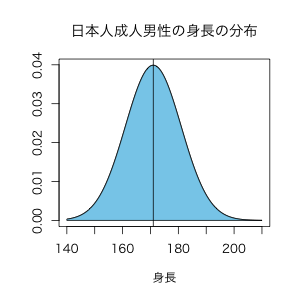
ここで１点注意点です。
このベル型の確率密度関数はあくまでも日本人の成人男性の身長を近似的に表しているだけなので、ベル型の確率分布（正規分布）に従う確率変数は実は-∞から+∞の値を取ります。そのため、期待値を計算するときは-∞から+∞で積分することになります。
ただし、上記のグラフを見て頂ければ分かる様に、100cmや250cmなどのまずあり得ないような極端な値が出る確率はほぼゼロです。
さて、それではこの日本人成人男性の身長Xが従う確率分布をベル型分布（正規分布）で近似したときの期待値E(X)は
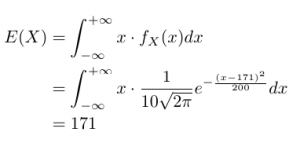
というように計算できます。
平均値171cmのベル型分布（正規分布）の期待値はちょうどその平均値である171cmにします。
途中の積分をどうやったのかというと、これを数学的にうまく積分しようとするとかなり難しいので、積分の定義を利用した「長方形近似」という手法を用いて近似的に求めました。長方形近似の詳細はここでは説明しませんが、「積分 長方形近似」などで検索して頂ければ参考になる説明が色々と出て来ます。
なお、長方形近似をRを用いて行うコードはプログラミングのページで公開します。
このように、期待値を数学的に計算することが難しいケースは非常に多いので、連続型の確率変数の期待値の計算は近似的な手法を用いることが非常に多いのです。
練習問題
0から１の値をとる連続型確率変数Xの確率密度関数が以下のように与えられているとき、Xの期待値E(X)を求めてみてください。
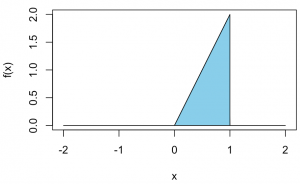
ちなみに、確率質量関数の定義に照らし合わせてみると、
•この関数は常に０以上の値をとり、
•この関数をXが取り得る領域で積分すると１になる（青い部分の面積が１）
（「確率密度関数、確率質量関数とは何か？」ページ参照。）
なので、この関数は確率密度関数であると言えます。
練習問題回答
この問題では、数学的な定義を用いて積分で期待値を求めることができるので、それをやってみましょう。
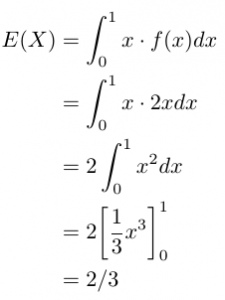
ということで、この確率変数Xの期待値E(X)は2/3であることがわかります。
