確率密度関数、確率質量関数とは何か？

確率分布を関数で表す。

確率論においてはよく、確率密度関数(Probability Density Function, PDF)、確率質量関数(Probability Mass Function, PMF)と呼ばれる関数を用いて確率分布を表現します。

確率密度関数は、連続型の確率分布を関数で表したもので、確率質量関数は離散型の確率分布を関数で表したものです。一般的に確率変数Xが従う確率密度関数または確率質量変数を $f_{X}(x)$ と表します。

まずは確率質量関数から見ていきましょう。

確率質量関数

確率質量変数は、離散型の確率分布を関数で表したものです。まずは例を見て見ましょう。

例：コインを２回振って何回表が出るか？

コインを２回振って表が出る回数を確率変数Xとします。Xが取り得る値はX={0,1,2}と一つずつ列挙することができるので、これは離散型の確率変数ですね。

そのコインを一回振ったときに表が出る確率を $p$ とすると、コインが歪んでいない前提で $p=1/2$ です。

さて、２回振ったうち２回とも裏がでる（X＝０）確率は1/4、１回だけ表が出る（X＝１）確率は1/2、２回とも表が出る（X＝２）確率は1/4ですね。

確率分布表を用いて以下のように表すことが出来るのでしたね。

確率分布表

表の回数X	確率
0	1/4
1	1/2
2	1/4
それ以外	0

また確率を表す $P$ の数式を用いて、

$\left \{ \begin{array}{l} P(X=0)=1/4\\ P(X=1)=1/2\\ P(X=2)=1/4\\ P(\neq0,1,2)=0 \end{array} \right.$

と表すことができました。

さて、この確率分布を確率密度関数を用いて表すと

$f_{X}(x)={}_2 C_{x}\big(\frac{1}{2}\big)^{x}\big(\frac{1}{2}\big)^{2-x}$

となります。

${}_2 C_{x}$ は２個の中から $x$ 個を選ぶとき、何通りの選び方があるか？を数式で表したもので「組み合わせ」と呼ばれます。これがわからない方は高校の数学Aの範囲の「組み合わせ」の概念を勉強しましょう。

$f$ の右についている大文字のXは、この関数は確率変数Xの分布を表す関数です、という意味です。

この関数にXが取り得る値{0, 1, 2}を代入することで、コインを２回振って０回表が出る確率、１回表が出る確率、２回表が出る確率をそれぞれ求めることができます。

それでは早速求めてみましょう！

まずX＝０、つまり、２回コインを振って０回表が出る（１度も表が出ない）確率は

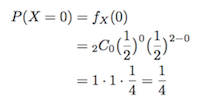
確率密度関数に代入することで、X＝０の確率が1/4だと得ることができましたね。

同じように、X＝１、X＝２の場合もやってみます。

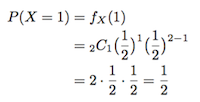
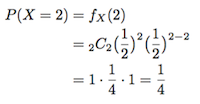
このように確率密度関数がわかれば、それに確率変数の値を代入して、その事象が起こる確率を求めることができます。

なお、この確率質量関数をグラフで表すと以下のようになります。

（Rコードを「図のタイトルを日本語表示する」ページで公開しています。）

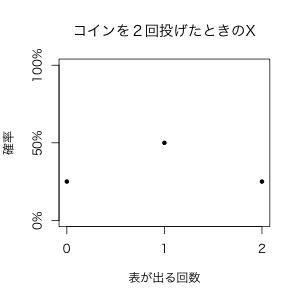
より一般化した確率質量関数

上記の例は表が出る確率が1/2のコインを２回振ったとき、という条件を付けましたが、

例えば歪んだコインがあって、表が出る確率が1/3しかないコインを５回振ったとき、４回表が出る確率を求めたいときにはどうすれば良いでしょうか？

実は上記の確率密度関数をより一般的な形で書くことにより、表が出る確率がどんな確率でも、また、コインを何回投げる場合であっても、この確率を求めることが可能です。

まずコインを振って表が出る確率を $p$ とおきます。この $p$ は割合（プロポーション）の $p$ ですね。
そして、コインを振る回数を $n$ とおきます。どういう意味があるのかは知りませんが、ナンバーの $n$ ですかね。

すると、表が出る確率が $p$ のコインを $n$ 回振って、 $x$ 回表が出る確率は

$f_{X}(x)={}_n C_{x}p^{x}(1-p)^{n-x}$

と表すことができます。

これで表が出る確率が何であっても、何回コインを投げても対応できますね。

また、この $p$ と $n$ をこの確率分布のパラメータと呼びます。コインを投げる回数や表が出る確率が変わった場合はこのパラメータを変えれば良いだけです。

それでは早速、表が出る確率 $p$ が1/3のコインを５回投げたとき( $n=5$ )、表が４回（X＝４）出る確率を求めてみると、

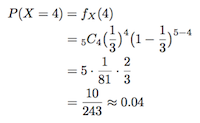
となります。約4%ということですね。

確率質量関数の性質

確率質量関数には以下の二つの性質があります。

確率質量関数の性質

1、Xがどんな値をとっても、 $f_{X}(x)$ は０以上である。

2、Xが取り得るすべての値の $f_{X}(x)$ を合計すると１になる。

つまり

1については、 $f_{X}(x)$ はXが各値をとるときの確率を表していて、確率は常に０から１の間であるため、この関数は常に０以上の値をとります。

例えば、上記のコインを投げる例で言うと、X＝0,1,2の確率はすべて０以上ですね。また例えばX＝３、つまり、２回コインを投げて３回表が出る、といったことはあり得ないので確率は０となります。つまり $f_{X}(3)=0$ となります。

２については、コインを２回投げたとき０回表が出る確率、１回の確率、２回の確率を合計すると、 $f_{X}(0)+f_{X}(1)+f_{X}(2)=1/4+1/2+1/4=1$ となり、合計は１になります。

なお、離散型の変数で、これらの二つの条件を満たすことが確質量度関数の定義であると考えて頂いて問題ありません。

確率密度関数

確率密度関数は連続型の確率分布を関数で表したものです。日本人成人男性の身長の例を見てみましょう。

例: 日本人成人男性の身長の分布を表す関数

日本人のように同質な集団の身長は一般的にベル型の分布をすると言われています。日本人成人男性の平均身長が大体171cmと言われていますので、身長の分布をグラフで近似的に表すと、以下の図のようになりますね。

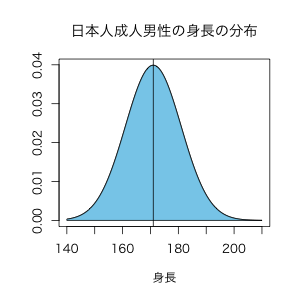
そしてこの分布の確率分布は、以下の確率密度関数で表すことができます。

$f_{X}(x)=\displaystyle{\frac{1}{{10 \sqrt {2\pi } }}e^{-\frac{(x-171)^2}{200}}}$

少し複雑に見えますが、関数電卓を持っている方は、この関数のグラフを描いてみてください。図のようなベル型のグラフになります。この”e”はネイピア数と呼ばれ、約2.718です。π(パイ)が約3.14なのはご存知かと思いますが、同じようにeは約2.718と考えて頂いて問題ありません。

ちなみにこれは正規分布という統計学の中でも最も有名な分布なのですが、正規分布の詳細については「確率論の基礎：正規分布とは何か？」のページで解説しますね。

さて、この確率密度関数から例えば身長160cmから180cmの人の割合がどれくらいいるか？といったことを求めるにはどのようにすればいいのでしょうか？

この確率変数は連続型なので、160cmから180cmの間で確率変数が取り得る値をすべて列挙してその確率を足し合わせる、といったことができません。

例えば

$f_{X}(160)+f_{X}(161)+f_{X}(162)+\cdots+f_{X}(180)$

としようとしても、この確率変数Xは連続型であるため、160.0000001や106.00000000000001など、160から180の間のすべての実数を列挙して確率を足し合わせることは不可能です。

そのため、連続型確率変数の確率密度関数を使って、ある値（ここでは160）からある値（ここでは180）までの確率を求めるにはこの確率密度関数を、求めたい値の間で積分します。

この場合で言えば、

$P(160\leq X \leq180)= \displaystyle{\int_{160}^{180} \frac{1}{{10 \sqrt {2\pi } }}e^{-\frac{(x-171)^2}{200}} dx}=0.68$

ですので、日本人成人男性の身長がこの確率密度関数に従うと仮定した場合、68％の人が160cmから180cmの間である、ということがわかります。

$P(160\leq X \leq180)$ というのは、確率変数X（つまり成人男性の身長）が160以上180以下の確率、という意味ですね。

ちなみに積分は高校数学II とIIIの範囲です。積分の概念は基本的な統計学を理解するのに必要ですので、これが全くわからない方は高校生の教科書などで学習することをお勧めします。

但し、概念だけある程度理解できれば大丈夫です。上記の積分の計算を電卓などを使わずに自力で解こうとすると、重積分と変数変換という大学生レベルの数学が必要になります。

このサイトでは「確率論の基礎」と「統計学の基礎」の項目については、重積分を使わず、高校数学までの知識で対応できる範囲を扱います。

（巷では、『数式を使わずに統計学を理解する』的な書籍に溢れていますが、ある程度しっかり統計学を理解するためには数学の知識は不可欠ですので、基礎的な数学の概念は学習するべきです。簡単そうな書籍で分かった気になっても応用が利きません。）

さて、上記の積分を図で表すと、以下のようにこの確率密度関数の下側の160と180に挟まれた部分の面積が、求める確率になります。

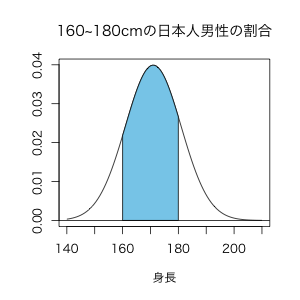
(Rコードを「関数の下の指定の定義域（ドメイン）部分に色をつける。」ページで公開しています。)

この青い部分の面積は0.68ですので、求める確率は68％であることがわかります。

同じように例えば、ランダムに一人の日本人成人男性の選んだ場合、その人の身長が180cm以上190cm以下である確率は以下のように確率密度関数を積分し、グラフの下の面積を求めることができますね。

$P(180\leq X \leq190)=\displaystyle{\int_{180}^{190} \frac{1}{{10 \sqrt {2\pi } }}e^{\frac{(x-171)^2}{200}} dx}=0.155$

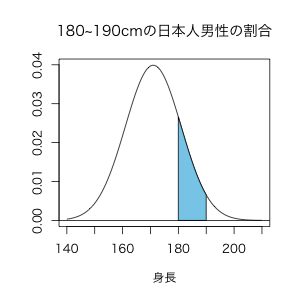
この青い部分の面積は0.155ですので、もとめる確率は15.5%であることが分かります。

確率密度関数の性質

確率密度関数には以下の二つの性質があります。

確率密度関数の性質

1、Xがどんな値をとっても、 $f_{X}(x)$ は０以上である。

2、Xが取り得る最小値から最大値で $f_{X}(x)$ を積分すると１になる。

つまり 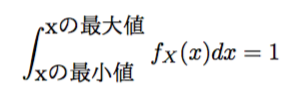screen-shot-2016-10-05-at-3-26-40-pm

1については、確率は常に０以上１以下の値しかとらないため、確率密度関数は常にプラスまたは0の値をとります。

2については、xが取り得る最小の値から、最大の値までを積分しますので、図で表すと、この確率密度関数の曲線の下側すべての部分です。

つまり、上の図の青い部分の面積は丁度１になるわけです。

練習問題

ある歪んだコインがあり、表が出る確率を $p=1/3$ とします。このコインを２回投げて表が出る回数を確率変数Xとするとき、X＝１となる確率、つまりコインを２回投げて１回だけ表が出る確率を確率質量関数を利用して求めてみてください。

練習問題回答

コインを２回投げるのでn=2です。そしてX＝１の確率を求めたいのでx=1をそれぞれ

$f_{X}(x)={}_n C_{x}p^{x}(1-p)^{n-x}$

に代入して、

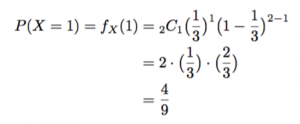
つまり、このコインを２回投げて、１回だけ表が出る確率は4/9と分かります。

MENU

確率分布を関数で表す。

確率質量関数

例：コインを２回振って何回表が出るか？

より一般化した確率質量関数

確率質量関数の性質

確率密度関数

例: 日本人成人男性の身長の分布を表す関数

確率密度関数の性質

練習問題

練習問題回答

確率論の基礎

スポンサー募集中。

更新・勉強会などの情報を受け取る。

理系の就職・職業訓練