分散、又は標準偏差とは何か？

確率変数の分散と標準偏差

確率変数の分散(Variance)とは、確率変数の分布のばらつきがどれくらい大きいかを示す0以上の数字です。

分散は英語でVariance(バリアンス)と呼ばれるため、確率変数Xの分散のことをVar(X)やV(X)などと表わします。

確率変数の標準偏差(Standard Deviation)とは、分散と同じく、確率変数の分布のばらつきがどれくらい大きいかを示す0以上の数字です。

分散と標準偏差は何が違うかというと、標準偏差は分散の平方根をとったものです。
一般的に確率変数の標準偏差はギリシャ文字のσ(シグマ)を用いて表わします。

つまり、確率変数Xの分散をVar(X)、標準偏差をσとすると、以下の関係が成り立ちます。

•分散= $Var(X)=\sigma^2$
•標準偏差 $\sqrt{Var(X)}=\sigma$

なぜわざわざ分散、標準偏差という二つの表し方があるのかというと、場合によってどちらかを使った方が都合が良いからです。例えば、分散の方が数学的に扱いやすいことが多いのに対し、標準偏差の方がその意味するところを解釈しやすい、といった特徴があります。

なぜ分散や標準偏差を考えることが重要か？

数字を読むトレーニングを受けていない人は、データを要約したり、理解しようとするときに、とかく平均値だけに目が行きがちです。

しかし、平均値だけを見ていると、実際に起こっている現象を誤って解釈してしまうことが多くあります。

例を見てみましょう。

例:学校ごとの統一テストの点数

例えばA高校では、ある統一テストの平均点が60点、B高校では平均点が45点だったとします。

高校	平均点
A高校	60
B高校	45

平均点は15点A高校の方が上回っているのですが、このデータからA高校の生徒の方がB高校の生徒より頭が良いと結論づけることができるでしょうか？
（哲学的にテストの点数で頭の良し悪しを計れるかどうかはここでは議論しません。単純にテストの点数が高い方が頭が良い、と定義します。）

これは平均値だけを見ても何とも言えません。それぞれの高校の生徒の点数がどれくらいばらついているか？を考慮する必要があるのです。

分散、標準偏差の数学的定義は後ほど述べますが、例えば以下のようにA高校の点数の分散が約7.3、標準偏差が約2.7、B両高校の点数の分散が約12.2、標準偏差が約3.5というように比較的ばらつきが小さいデータが得られたとします。

高校	平均点	分散	標準偏差
A高校	60	7.2	2.7
B高校	45	12.0	3.5

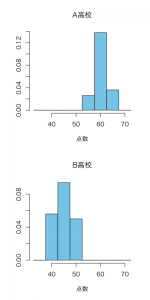
上の図を見比べて頂ければ分かるように、このケースでは

A高校の生徒はほとんどが、60点前後であり、最も低い点数の人たちでも55点前後なのに対し、
B高校ではほとんどの生徒が45点前後で、最も点数の高い人たちが55点前後取ということがわかります。

つまりこの例では圧倒的にA高校の生徒の方が頭が良いことがわかります。

次に平均点は今までと同じA高校約60点、B高校約45点でも

B高校の点数のばらつきが非常に大きく、以下のようにA高校の点数の分散が約7.3、標準偏差が約2.7、B両高校の点数の分散が約324、標準偏差が約18というデータが得られたとします。

高校	平均点	分散	標準偏差
A高校	60	7.2	2.7
B高校	45	330	18

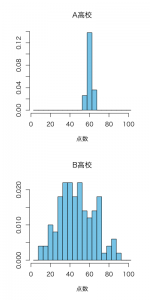
この場合、前の同じく平均値はA高校の方がずっと上ですが、B高校には80点を超える生徒たちもおり、校内トップ層はB高校の方がA高校よりも頭が良いことになります。

一般的に高校が進学先の大学リストに載せたいような有名大学などに進学できるのはこの統一テストで80点以上をとるような生徒たちですから、受験においてはB高校の方がA高校よりも良い高校とみなされることでしょう。

このように、データの背後にある現象を考察する際には、平均値だけを見ていると誤った解釈をしてしまうことが非常に多いので、分散、標準偏差といったデータのばらつき度合いも合わせて考えるようにしましょう。

確率変数の分散、標準偏差の数学的定義

確率変数Xの分散と標準偏差の数学的定義は以下の通りです。

確率変数Xの分散と標準偏差の数学的定義

•分散

(1) $Var(X)=\sigma^2=E\big[(X-E(X))^2\big]$
(2) $Var(X)=\sigma^2=E(X^2)-\big[E(X)\big]^2$

•標準偏差

$\sigma=\sqrt{Var(X)}$

確率変数の分散の定義は(1)ですが、(1)の式を変形して(2)を得ることができます。
（式の変形の仕方などは「確率論の基礎」の範囲内では扱いません。要望が多ければ別のセクションでもう少し数学的に解説したいと思います。）

また(2)の方が実際に確率変数Xの分散を計算する際に使い勝手が良いです。以下で確率変数の分散と標準偏差を計算する例を見てみましょう。

例: サイコロの目の分散

歪んでいないサイコロを１回振った時に出る目を確率変数Xとしたとき、このXの分散Var(X)と標準偏差σを求めてみます。

分散を求めるために、上述した分散の定義(2) $E(X^2)-\big[E(X)\big]^2$ を使います。

サイコロは歪んでいないと仮定しているので、Xの確率分布は以下のようになりますね。

確率分布表

出る目	確率
1	1/6
2	1/6
3	1/6
4	1/6
5	1/6
6	1/6
それ以外	0

さて、まずE(X)は

$1\times\frac{1}{6}+2\times\frac{1}{6}+3\times\frac{1}{6}+4\times\frac{1}{6}+5\times\frac{1}{6}+6\times\frac{1}{6}=\frac{21}{6}=3.5$

となりますので、E(X)=3.5と求めることができます。

（この期待値の求め方は「期待値とは何か？」のページで詳しく解説しています。）

次に $X^2$ の期待値（ $E(X^2)$ ）を求める必要があります。そのためにはX²を一つの確率変数と考えてX²の期待値を求めます。

確率変数 $X^2$ は以下のように分布しますね。

確率分布表

X	X²	確率
1	1	1/6
2	4	1/6
3	9	1/6
4	16	1/6
5	25	1/6
6	36	1/6
それ以外		0

期待値の定義に従って、確率変数 $X^2$ の期待値は以下のように計算できます。

$E(X^2)=1\times\frac{1}{6}+4\times\frac{1}{6}+9\times\frac{1}{6}+16\times\frac{1}{6}+25\times\frac{1}{6}+36\times\frac{1}{6}=\frac{91}{6}\approx15.17$

さて、これを分散と標準偏差の公式に代入すれば

• $Var(X)=E(X^2)-\big[E(X)\big]^2=15.2-3.5^2=15.17-12.25=2.92$
• $\sigma=\sqrt{Var(X)}=\sqrt{2.92}\approx1.7$

つまりこの確率変数Xの分散は2.92、標準偏差は1.7と求めることができます。

ですので、このサイコロを何度も振り続けると、出た目の分散は2.92に近づいていきます。

母集団の分散と標準偏差

さて、上記では確率変数の分散や標準偏差の求め方を学びましたが、実際にあなたが集団やデータのばらつき具合を調べたい時は、上記の例のように確率分布が与えられているのではなく、

例えば、

•「教えているクラスのテストの点数のばらつきを計算したい」とか、
•「会社内の従業員全員の年収のばらつきを知りたい」とか、

実際のデータが数字として与えられていて、その分散や標準偏差を計算したいケースが多いと思います。

このように母集団のデータが与えられているときの分散、標準偏差は以下のように計算します。

※1「母集団」とは、分析対象の集団全員からなる集団のことを指します。例えば、A高校の生徒の統一テストのばらつき具合を調べたい時、この場合の母集団は「A高校の生徒全員」ということになります。
※2 「母集団」と「標本」の違いなどの概念については「統計学の基礎」の中で解説します。

母集団の分散と標準偏差の数学的定義

n個のデータからなる母集団があって、その各数字を $x_{1},x_{2},\cdots,x_{n}$ とします。さらに、その母集団の平均値をμとすると、その分散σ²は

$\sigma^2=\displaystyle{\frac{(x_1-\mu)^2+(x_2-\mu)^2+\cdots+(x_n-\mu)^2}{n}}$

と定義されます。

標準偏差σは、この分散σ²の平方根をとって以下のように表すことができます。

$\sigma=\sqrt{\sigma^2}=\displaystyle{\sqrt{\frac{(x_1-\mu)^2+(x_2-\mu)^2+\cdots+(x_n-\mu)^2}{n}}}$

つまり日本語で表すと、分散とは「母集団の各値からその平均値μを引いたものを二乗し、それらの平均値をとったもの」、と言うことができます。

ここでするどい人からは「なぜばらつきを２乗するのか？各値と平均値の差の絶対値ではだめなのか？」という質問を受けます。

この理由は主に２つ。

ひとつは、絶対値がつく値は数学的に取り扱いにくいこと。
もうひとつは、多くの統計学や確率論の理論がこの定義に従ってすでに構築されていることです。

例: ある母集団の分散を求める。

それでは実際に母集団となるデータが与えられているとして、その分散を求めてみましょう。

例えば、ある小さい会社の営業部の営業部全員（6人）の月収は以下の通りです。

確率分布表

営業部	月収
部長	150万円
課長	80万円
Aさん	35万円
Bさん	35万円
Cさん	30万円
Dさん	30万円

この6人の平均月収はμ=60万ですから、この分散σ²と標準偏差σを求めると

分散= $=\sigma^2=\displaystyle{\frac{(150-60)^2+(80-60)^2+(35-60)^2+(35-60)^2+(30-60)^2+(30-60)^2}{6}\times(10000)^2}=192,500,000,000$

標準偏差= $\sigma=\sqrt{\sigma^2}=\sqrt{192500000000}\approx440,000$

つまり、分散(σ²)は1925(万x万)=1925億、標準偏差(σ)は約44万円となります。

通常、分散の方が標準偏差に比べて数学的に扱いやすいことが多いのですが、実際にその意味するところを解釈する際は、このように標準偏差の方が分かりやすいのです。

練習問題

別の小さい会社の営業部全員（6人）の月給が以下の通り与えられているとき、この分散を求めてみましょう。

確率分布表

営業部	月収
部長	90万円
課長	70万円
Aさん	50万円
Bさん	50万円
Cさん	50万円
Dさん	50万円

練習問題回答

この6人の平均月収は $\mu=\displaystyle{\frac{90+70+50+50+50+50}{6}\times10000}$ =60万ですから、この分散σ²と標準偏差σを求めると

分散= $\sigma^2=\displaystyle{\frac{(90-60)^2+(70-60)^2+(50-60)^2+(50-60)^2+(50-60)^2+(50-60)^2}{6}\times(10000)^2}\approx23,300,000,000$

標準偏差= $\sigma=\sqrt{\sigma^2}=\sqrt{233\times(10000)^2}\approx150,000$

つまり分散は約233億、標準偏差は約15万円となります。前の例も、この練習問題でも営業部6人の月収の平均は同じ60万円ですが、前の例が標準偏差44万円とかなりばらつきが大きいのに対し、この例では標準偏差15万円と比較的ばらつきが小さく、全員が一定水準のよい給料をもらっていることがわかります。

なお、仮に母集団のデータがすべて同じ場合、つまりこの例では全員の給料が同じ場合は分散=標準偏差=0となります。

MENU

確率変数の分散と標準偏差

なぜ分散や標準偏差を考えることが重要か？

例:学校ごとの統一テストの点数

確率変数の分散、標準偏差の数学的定義

例: サイコロの目の分散

母集団の分散と標準偏差

例: ある母集団の分散を求める。

練習問題

練習問題回答

確率論の基礎

スポンサー募集中。

更新・勉強会などの情報を受け取る。

理系の就職・職業訓練