「相関関係」と「相関係数」は一見、簡単に理解できそうですが、
実は間違って解釈をされていることが非常に多い統計学の用語です。
今回は、相関関係、相関係数、疑似相関とは何か？
また、よくある間違いを犯さないための注意点を解説していきます。
知っているか知らないかで、メディアを見て騙されるか、見抜けるかが
決まると言っても過言ではないコンセプトですので、おさえておきましょう。
【目次】
相関関係とは何か？
-時給の例
-営業マンが働いた日数と売り上げの関係
-高いところから球を落とした場合の時間（秒）と落下距離の関係
相関係数とは何か？
-相関係数の計算の仕方
-1,時給の例の相関係数。
-2,営業マンが働いた日数と売り上げの相関係数
-3,高いところから球を落とした場合の時間（秒）と落下距離の相関係数
疑似相関とは何か？
練習問題
練習問題回答
相関関係とは何か？
一般的には相関関係とは
「2つの変数において一方の変数が増えるにつれて、もう一方の変数も増える（または減る）関係」
と考えられています。
しかし、同時に「相関関係」は英語では”Correlation”と訳されます。
英語でCorrelationと言った場合、
「2つの変数に（直線の）線形の関係」があることを指します。
日本語の「相関関係」を英語で言いたい場合、”Association”と
言う方が正しいです。
“Association”と言った場合は、「直線的な関係」という意味は特になく、
2つの変数が曲線的に関連しているケースを含みます。
例を示します。
時給の例
あなたが時給1000円で働くアルバイト店員だとしましょう。
この場合、働いた時間が増えるごとに、直線的に稼ぎが増えます。
グラフにすると以下のようになりますね。
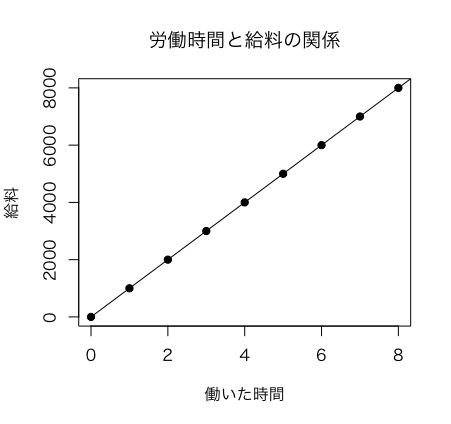
この例の場合は、働いた時間と給料は、まったくばらつきのない、完全な相関関係があります。このような完全な相関関係がある場合は、すべての点が直線上に並びます。
営業マンが働いた日数と売り上げの関係
上記の時給の例では、時給と給料の関係は全くばらつきがなく、「給料＝労働時間x1000円」の式で表すことができました。
しかし、多くのケースにおいて二つの変数がこのように完全な相関関係を持っているわけではありません。
例えば、30人の営業マンを分析して、１ヶ月に働いた日数と、売り上げの関係が以下のようになったとしましょう。
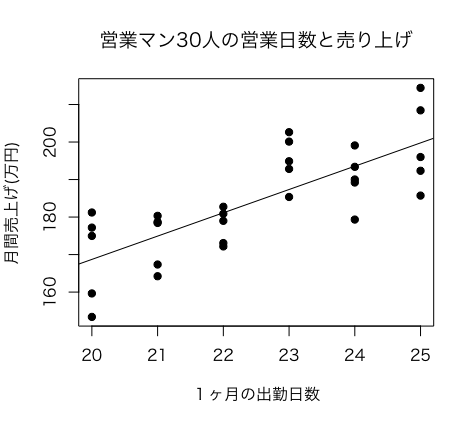
この場合も、営業日数の多い営業マンほど売り上げも直線的に増加する相関関係があります。
ただし、同じ日数、仕事をした人が皆、同じ売り上げが上がるわけではなく、売り上げに多少のばらつきがあります。そのため、各点（データポイント）は直線上に並ばず、直線の上下に分布します。
高いところから球を落とした場合の時間（秒）と落下距離の関係
高いところから球を落とした場合のt=1,2,3,4,5,6,7秒後の落下距離を
とすると、時間と落下距離の関係は”曲線的”な関係があります。
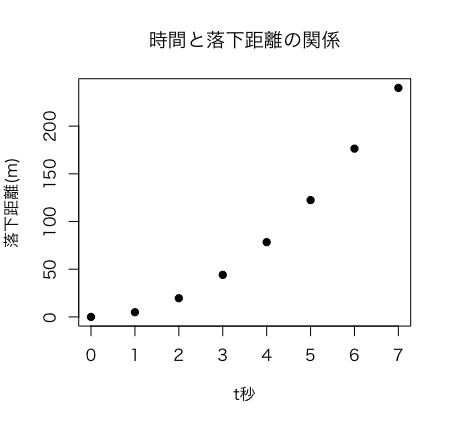
このケースの場合では、確かに時間が経過するに連れて、距離が伸びるという意味では、日本語で通常言われる相関関係があると言えます。
しかし、以下にて相関係数の項目でも触れますが、このケースでは、「時間と距離の関係にばらつきがない」のにもかかわらず、データに直線を引いた場合、データポイントは直線上に並びません。
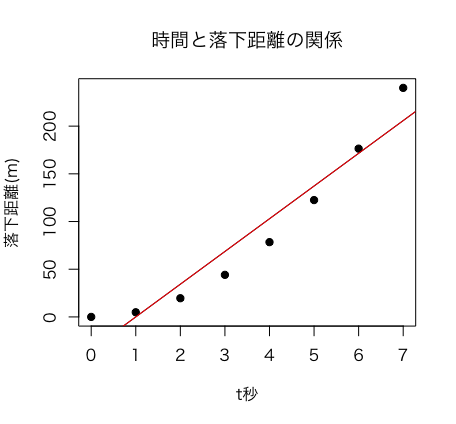
このように「相関関係」を英語で表した”Correlation”は、2つの変数の直線的な関連性のことを言いますので、この場合は完全な相関関係にはなりません。
相関係数とは何か？
相関係数とは、２つの変数の直線的な相関関係の強弱を-1から1の間で表したものです。標本の相関係数(r)は以下の公式で求められます。
なお、サンプルにおける相関係数はrで表しますが、母集団における相関係数は
相関係数が１のとき、2つの変数の間にはばらつきの全くない完全な正の相関があり、相関係数が−１のとき、完全な負の相関があります。
「正の相関」とは、一つの変数が増えるに連れて、もう一方も増えること、「負の相関」とは、一つの変数が増えるに連れて、もう一方が減ることを意味します。
相関係数が０のとき、2つの変数には相関関係がありません。つまり、一つの変数が増えても、もう一つの変数が変わらないことを意味します。
相関係数の絶対値が１に近くに連れて、相関関係が強くなります。
相関係数の公式は多少複雑なので、通常はエクセル(=CORREL()関数)やR(cor()関数)、Python（np.corrcoef()関数）などのソフトウェアなどを利用して計算します。
まずは簡単な例で相関係数の求め方を説明した後、上記で見てきた例の相関係数をソフトウェアを利用して求めてます。
相関係数の計算の仕方
それでは４人の生徒の数学と英語のテストの点数が以下のようになっているとき、相関係数を求めてみます。
| 数学 | 100 | 90 | 80 | 60 |
| 英語 | 90 | 60 | 75 | 65 |
まず、数学の点数を変数xとして、英語の点数を変数yとすると、数学の点数の標本平均は
82.5と計算できます。同じように、英語の点数の標本平均は
次に相関係数の公式の分子と分母をそれぞれ計算します。
分子＝
分母＝
r＝相関係数＝375/644.69＝0.55.
1,時給の例の相関係数。
| 働いた時間 | 給料 |
| １時間 | 1,000円 |
| ２時間 | 2,000円 |
| ３時間 | 3,000円 |
| 4時間 | 4,000円 |
| 5時間 | 5,000円 |
| 6時間 | 6,000円 |
| 7時間 | 7,000円 |
| 8時間 | 8,000円 |
この場合は、労働時間と給料の2つの変数の間に全くばらつきのない正の相関があるので、相関係数は１となります。
2,営業マンが働いた日数と売り上げの相関係数
| 出勤日数（日） | 月間売り上げ（万円） |
| 20 | 153, 177, 181, 175, 160 |
| 21 | 180, 167, 179, 164, 178 |
| 22 | 172, 179, 183, 173, 181 |
| 23 | 193, 203, 200, 185, 195 |
| 24 | 179, 190, 193, 189, 199 |
| 25 | 192, 214, 208, 196, 186 |
このケースでは、エクセルやRなどの関数を使って相関係数を求めるとr=0.773となります。相関係数が正で、１に近いのでこれは「やや強い正の相関」があると言えます。
なお、相関係数がいくつ以上であれば強い相関、いくつ以下であれば弱い相関なのか？といった絶対的な基準はありません。
3,高いところから球を落とした場合の時間（秒）と落下距離の相関係数
| 時間 | 落下距離 |
| 0秒 | 0 |
| 1秒 | 4.9m |
| 2秒 | 19.6m |
| 3秒 | 44.1m |
| 4秒 | 78.4m |
| 5秒 | 122.5m |
| 6秒 | 176.4m |
| 7秒 | 240.1m |
このケースでは、相関関係を求めるとr=0.96となります。
この時間と距離は全くばらつきがない曲線的な関係にあるため、「直線的な」相関係数を求めると完全な正の相関関係であるr＝１にはならないのがお分かり頂けると思います。
疑似相関とは何か？
疑似相関とは、２つの変数の間に交絡因子により因果関係があるように見えることを言います。
通常のメディアやニュースなどで、
「コーヒーを飲む人はガンの発症率が低い」とか、
「朝食を抜くひとは、脳出血の発症率が高い」とか、
「女性の就業率高い社会では離婚率が高い」
といった相関関係があたかも因果関係のように取り上げられていますが、これらは、統計学的に因果関係を結論づけることはできません。
例えば、「女性の就業率高い社会では離婚率が高い」に関しては、女性への教育が進んでいるという交絡要因があるかもしれません。
これらの統計学的な因果関係の結論付けや、交絡要因に関しての詳細は「統計学を用いた因果関係の結論付け。観察研究/実験研究/ランダム化比較試験」をお読みください。
練習問題
１、５人の身長と体重が以下のように与えられているとき、相関係数を求めてください。
２、この相関係数を見て、身長が高いことが体重が多いことの間に、因果関係があることを統計学的に結論づけることができますか？
| 身長 | 体重 |
| 160cm | 60kg |
| 165cm | 70kg |
| 170cm | 75kg |
| 175cm | 75kg |
| 180cm | 90kg |
練習問題回答
1, r = 0.948
2, 因果関係を結論づけることはできない。
