xの範囲ごとに違う関数を利用したい場合
統計学における確率密度関数では、xが取り得る値以外が起こる確率は0であるため、
xがある範囲[a,b]に含まれる場合は関数f(x)の値をとり、それ以外は0の値をとる、
といった場合分けをした関数のグラフを描きたいことが多々あります。
例えば「期待値とは何か?」のページの練習問題で以下のような確率密度関数を考えました。
このケースではxの定義域が[0,1]の間なので、xが0以外の値をとる場合の確率は0です。
しかし、普通に以下のようにRでプログラムを書くと、定義域ごとの場合分けができていないため、欲しい結果が得られません。
f=function(x){
return(2*x)
}
curve(f(x),xlim=c(-2,2),ylim=c(-2,2), asp=1,
main="",
ylab="f(x)",
col="red")
abline(h=0)
abline(v=0)
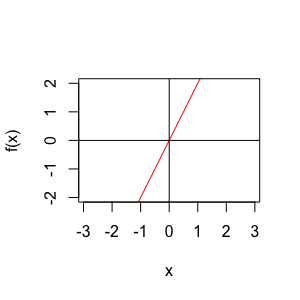
上記のようにxの範囲が-∞から∞になってしまうので、プログラミングをする際は以下のようにまずはif()関数を使って、xの定義域ごとに確率密度関数f()がとる値を分けます。
f=function(x){
if (x<=0){f=0}
else if (x>=1){f=0}
else {f=2*x}
return(f)
}
次に、以下のVectorize()関数を利用して、確率分布の関数f()をベクトル化して、関数曲線を描くcurve()関数の中に入れます。
h=Vectorize(f)
curve(h,xlim=c(-2,2),
ylim=c(0,2),
asp=1,
main="",
ylab="f(x)")
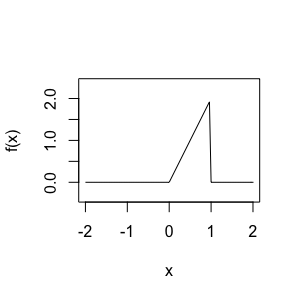
これで定義域ごとに違う関数の値をとるグラフを描くことができました。
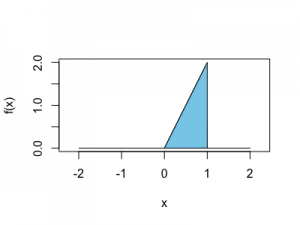
最後に以下のように指定の範囲にスカイブルーの色をつけて出来上がりです。
x=c(0,seq(0,1,length=100),1) y=2*x cord.x=c(0,x,1) cord.y=c(0,y,0) polygon(cord.x,cord.y,col='skyblue')
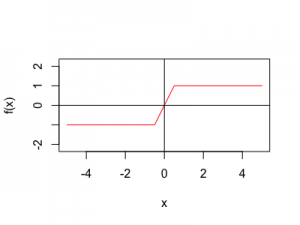
次にxが[-∞,0],[0,1],[1,∞]ごとに違う関数の値をとる以下のような関数のグラフをかいてみます。
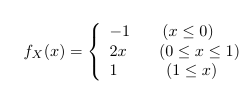
上で述べた手法を応用すれば、下記のコードでグラフを描くことができます。
f=function(x){
if (x<=-1/2){f=-1}
else if (x>=1/2){f=1}
else {f=2*x}
return(f)
}
h=Vectorize(f)
curve(h,xlim=c(-5,5),ylim=c(-2,2), asp=1,
main="",
ylab="f(x)",
col="red")
abline(h=0)
abline(v=0)