Rコード:数値積分（長方形近似）で関数を積分する。

Tweet

長方形近似で関数を積分するコード

統計学では期待値を求める際などに頻繁に積分を用いますが、多くのケースでは、数学的に積分するのが難しすぎる、または、不可能なので、長方形近似などの手法を用いて近似的に値を求めることがあります。

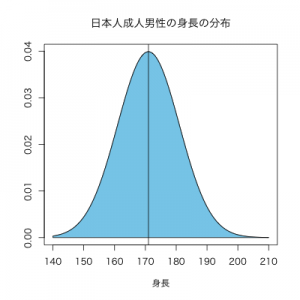
「期待値とは何か？」のページでは、以下の平均値171、標準偏差10の分布の期待値を求める際に、長方形近似を利用しました。

•確率密度関数

•グラフ

•期待値の求め方

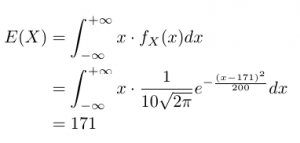
上記を計算しようとするとかなり複雑になるため、長方形近似を利用したのでしたね。

まず、この正規分布の関数の平均値をμ、標準偏差をσとして、下記のようにこの確率密度関数normal.func()を定義しました。正規分布の定義やその確率密度関数に関しては、「確率論の基礎」の中で解説します。

•コード

# 正規分布の関数
normal.func=function(mu,sd,x){
  f=(1/(sd*sqrt(2*pi)))*exp(-(x-mu)^2/(2*sd^2))
  return(f)
}

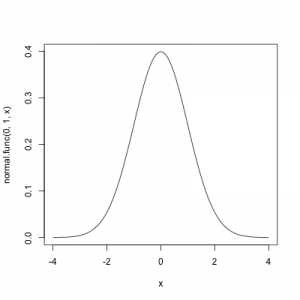
ちなみに上記で作成したnormal.func()関数を用いて、たとえば、平均値μ=0、標準偏差σ=1の正規分布のグラフを描きたければ、curve()関数を利用し、

#この関数のグラフを描く。
curve(normal.func(0,1,x),-4,4)

とすれば、以下のようにグラフを描くことができます。

さて、期待値を求めるためには

ではなく、

を積分しなければいけないので、この関数をRで定義すると以下のようになります。

•コード

# x掛けるnormal.func
#muは平均値。
#sdは標準偏差。
normal.expected=function(mu,sd,x){
  f=x*(1/(sd*sqrt(2*pi)))*exp(-(x-mu)^2/(2*sd^2))
  return(f)
}

さて本題に入ります。この確率変数Xの期待値E(X)を求めるには上記のnormal.expected()関数に平均値μ=171、標準偏差σ=10を代入した関数を、-∞から+∞で積分します。

以下が関数normal.expected()をaからbの間で積分する関数です。この関数をintegral()と名付けます。

•コード

#長方形近似を用いて積分を近似的に求める。
integral=function(a,b,k){
  inte=rep(NA,k-1)
  for (i in 1:k-1){
    inte[i]=((b-a)/k)*normal.expected(171,10,a+((b-a)/k)*(i-1))
  }
  return(sum(inte))    
}

それではこの関数を利用して実際に期待値を求めてみます。

ただし、現実的にはRでマイナス無限大から無限大までを積分する設定ができないので、ここでは、関数が取り得る値を十分にカバーできるように、０から500の間で長方形近似を用いて積分してみます。

integral(0,500,10000)

この10000は０から500の値の範囲を10000個の長方形に分割して値を近似するという意味です。

さて実際に実行すると、

> integral(0,500,10000)
[1] 171


と表示され、（ほぼ）正しい期待値が表示されます。

なお、Xが別の連続型に従う分布の場合は、integral()関数の内部で利用するnormal.expected()関数をご自分で作って頂ければ、その期待値E(X)を求めることが可能です。

是非、ご利用ください。

Tweet