PythonでF検定（等分散性の検定）を行う方法 (Pythonによる統計学入門)

Tweet

今回はPythonを用いて等分散性の検定（F検定）を行う方法を解説します。

等分散性の検定では2つのグループの分散（または標準偏差）が違うかどうかをF検定を用いて結論づけることができます。

仮説は以下のようになります。

: 二つの群の分散は等しい。

: 二つの群の分散は違う。

例えばt検定を利用する際に、二つのグループの分散が違うのであれば
ウェルチのt検定を利用することが多いのですが、

二つのグループの分散が違うかどうかを判断するために、
このこの等分散性の検定（F検定）を利用することができます。

Pythonを用いてこの等分散性の検定をするために、
まずは以下のように必要なライブラリをインポートしましょう。

# 必要なライブラリをインポート
import numpy as np　#数値計算を行うためのライブラリ
import scipy #等分散性の検定(F件検定)を行うためのライブラリ
import matplotlib.pyplot as plt　#ヒストグラムを描くのに利用
import statistics as stat　# 標本分散の計算に利用

例えば、日本人のアメリカ人の成人男性の身長の分散が
違うと言えるかどうかを検定してみたいと思います。

以下のように、日本人とアメリカ人の成人男性を30人づつ
抽出して、身長を測定します。

# 日本人男性30人をサンプル
np.random.seed(1)
Japan = np.round([np.random.normal(171, 6, 30)],1).reshape(30)

# アメリカ人男性30人をサンプル
np.random.seed(1)
US = np.round([np.random.normal(180, 8, 30)],1).reshape(30)

この標本抽出にあたって、日本人の平均身長を171cm、標準偏差を６、
アメリカ人の平均身長を180cm、標準偏差を８と仮定しました。

それぞれのグループの標本分散を求めてみます。

# 標本分散
stat.variance(Japan)
stat.variance(US)

>>> stat.variance(Japan)
37.972195402298865
>>> stat.variance(US)
67.518896551724112

このように日本人の身長の標本分散は約38、
アメリカ人の標本分散は約67.5とでました。

この数字だけを見ると、二つのグループの分散は違うような気もします。

次に以下のコードで各グループの身長のヒストグラムを
比べてみましょう。

# 分散を比べるヒストグラム
fig = plt.figure()
ax = fig.add_subplot(111)
ax.hist(Japan, bins=15, normed=True, color='red', alpha = 0.7) #日本人ヒストグラム
ax.hist(US, bins=15, normed = True, color='blue', alpha = 0.7) #アメリカ人ヒストグラム
ax.set_title('Japanese:Red   American:Blue') #図のタイトル
ax.set_xlabel('height') #x軸タイトル
ax.set_ylabel('proportion') #Y軸タイトル
fig.show()

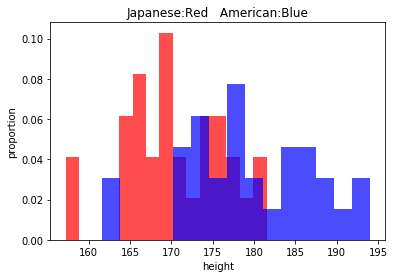
このヒストグラムを見ると各グループの分散はそれほど違わないようにも見えますね。

それでは、正式に等分散性の検定（F検定）を行います。

# 等分散性の検定を行う。
scipy.stats.bartlett(Japan,US)

scipy.stats.bartlett()関数を利用し、カッコの中に
各グループの身長が格納されたベクトルを入れるだけです。

結果は以下のようになります。

>>> scipy.stats.bartlett(Japan,US)
BartlettResult(statistic=2.3290558523567992, pvalue=0.1269788727635183)

P値が0.127となりますので帰無仮説を棄却することができません。
つまり、二つのグループの分散が違うとは結論付けられません。

※この記事を書くのに以下のページを参考にしました。
– https://docs.scipy.org/doc/scipy-0.14.0/reference/generated/scipy.stats.bartlett.html
– https://docs.python.org/3/library/statistics.html

Tweet