Pythonを用いて線形回帰分析(単回帰、重回帰)を行う
今回は、Pythonを用いて線形回帰を行う方法をご紹介します。
回帰分析は、統計学的モデリングの最も基本的なもので、
Pythonを用いて簡単に実行することができます。
回帰分析では、説明変数と応答変数の直線的な関係をモデリングします。
1つの説明変数を統計モデルに含む場合には「単回帰分析」、
2つ以上の説明変数を含む場合は「重回帰分析」と呼びます。
【目次】
利用するデータセット
データの読み込み
散布図を描いてデータをチェック
Pythonによる単回帰分析
Pythonによる重回帰分析
利用するデータセット
今回は、以下の
Applied Linear Statistical Modelsの中で例として挙げられているデータセットを利用します。
なお、この教科書は約1400ページあり、実用的な線形モデルの使い方から、
統計学の数学的理論まで含めてガッチリと解説されているので、
網羅的に学習したい方にはオススメです。
ちなみに以下のリンクからpdfバージョンを見る事もできます。
https://mysite.science.uottawa.ca/rkulik/mat3378/mat3378-textbook.pdf
今回利用するデータは以下のページで公開されています。
線形回帰練習用データ
データの読み込み
さて、Pythonでデータを読み込み分析をするために、
以下のようにライブラリを読み込みます。
import os # ディレクトリを設定するためのライブラリ import pandas as pd # Pythonでデータフレームを扱う(panda package) import statsmodels.formula.api as sm # 回帰分析のライブラリ import seaborn # 散布図に回帰直線を引くライブラリ
今回は、データファイルをdata.csv、変数の名前をそれぞれ
X1, X2, Yと名付けました。
以下のようにpandasライブラリのread_csv関数を用いてデータを読み込みます。
# CSV形式のデータを読み込む
mydata = pd.read_csv('ファイルのパス/data.csv', delim_whitespace=True)
散布図を描いてデータをチェック
線形回帰分析では、説明変数と応答変数が直線的な関係があると考えて
モデル構築をするケースが多いので、
ここでは散布図を描いて各説明変数(X1,X2)と応答変数(Y)の
関係を視覚的に見てみます。
Pandasライブラリを利用して以下のように
散布図を描くことができます。
# pandasライブラリを利用して散布図を描く mydata.plot.scatter(x='X1', y='Y', title='X1 vs Y') mydata.plot.scatter(x='X2', y='Y', title='X2 vs Y')
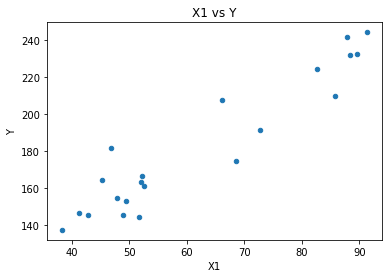
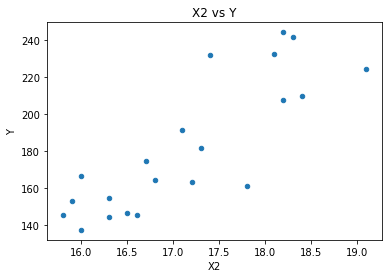
散布図を見るとX1もX2も両方ともYと直線的な関係があることが分かります。
それでは、単回帰分析と重回帰分析を行っていきましょう。
Pythonによる単回帰分析
単回帰分析では説明変数は一つです。X1とYの関係、X2とYの関係を
それぞれ以下のモデルで表します。
それでは早速、Pythonを利用して単回帰分析を行います。
# 単回帰モデル1 SLR1 = sm.ols(formula="Y ~ X1", data=mydata).fit() print(SLR1.summary()) # 単回帰モデル2 SLR2 = sm.ols(formula="Y ~ X2", data=mydata).fit() print(SLR2.summary())

X1の行のP値(P>|t|)は0.000となり、非常に小さいのでこの単回帰モデル1において説明変数X1の効果は統計的に有意であると言えます。
また、回帰係数の95%の信頼区間は[1.529, 2.142]となります。
散布図上に回帰直線を引きたい場合は以下のコードで可能です。
# 散布図に回帰直線を入れる seaborn.lmplot(x='X1',y='Y',data=mydata,fit_reg=True)
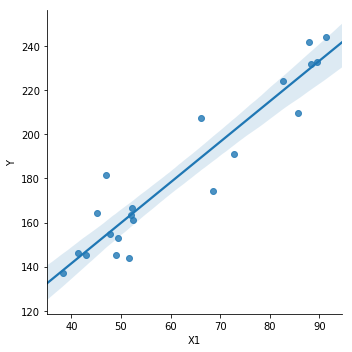
単回帰モデル2も全く同じように分析できますので、
ぜひ、試して見てください。
Pythonによる重回帰分析
重回帰分析では2つ以上の説明変数と、
応答変数の関係をモデリングします。
今回は以下のようにモデルを構築してみます。
それでは、重回帰分析のモデルを実装します。
# 重回帰分析 MLR = sm.ols(formula="Y ~ X1 + X2", data=mydata).fit() print(MLR.summary())

X1の行のP値が0.000, X2の行のP値が0.033となり、
この重回帰分析モデルにおいて、どちらの変数も
有意な効果があると言えます。
※この記事を書くのに参考にしたページ
– pandas.read_csv
https://pandas.pydata.org/pandas-docs/stable/generated/pandas.read_csv.html
– https://www.statsmodels.org/stable/index.html


