当ページではPythonを用いて二つの母集団における平均値に差があるかどうかの統計的仮説検定(t検定,Welchのt検定)を行う方法を紹介します。
なお、統計的仮説検定、P値、有意差、t検定については既に学習をしているものとしますので、これらの概念に自信がない方は、「統計学の基礎」のセクションで学習してください。
まずは、必要なライブラリをインポートします。
import numpy as np #数値計算を行うためのライブラリ import matplotlib.pyplot as plt #ヒストグラムを描くのに利用 from scipy import stats # t検定に利用
今回は日本人とアメリカ人の成人男性を10人づつランダムにサンプリングして、平均身長に差があるかどうかを結論づけることができるか検定してみましょう。
以下のコードで日本人とアメリカ人10人づつを抽出します。
# 日本人男性10人をサンプル np.random.seed(1) Japan = np.round([np.random.normal(171, 6, 10)],1).reshape(10) # アメリカ人男性10人をサンプル np.random.seed(1) US = np.round([np.random.normal(180, 8, 10)],1).reshape(10)
抽出された日本人10人の身長:
>>> print(Japan)
[ 180.7 167.3 167.8 164.6 176.2 157.2 181.5 166.4 172.9 169.5]
抽出されたアメリカ人10人の身長
>>> print(US)
[ 193. 175.1 175.8 171.4 186.9 161.6 194. 173.9 182.6 178. ]
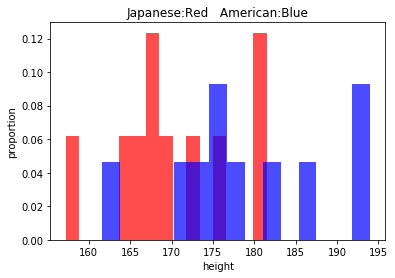
以下のコードで抽出された日本人とアメリカ人10人づつの身長の分布を確認することができます。
# ヒストグラムを比べる
fig = plt.figure()
ax = fig.add_subplot(111)
ax.hist(Japan, bins=15, normed=True, color='red', alpha = 0.7) #日本人ヒストグラム
ax.hist(US, bins=15, normed = True, color='blue', alpha = 0.7) #アメリカ人ヒストグラム
ax.set_title('Japanese:Red American:Blue') #図のタイトル
ax.set_xlabel('height') #x軸タイトル
ax.set_ylabel('proportion') #Y軸タイトル
fig.show()
それでは早速、t検定を行ってみます。
# t検定 (等分散 、両側検定) stats.ttest_ind(Japan,US, equal_var = True)
ここでは「equal_var = True」を指定することにより、日本人男性とアメリカ人男性の身長の分散が等しいことを仮定しています。

P値が0.039となり、帰無仮説を棄却することができます。
次に二つのグループの分散が等しいと仮定できない場合に行うWelchのt検定を行ってみましょう。
# t検定 (非等分散 Welchのt検定、両側検定) stats.ttest_ind(Japan,US, equal_var = False)

P値が0.04となり、この場合も帰無仮説を棄却することができます。
※記事を書くのに以下のページを参照しました。
scipy.stats.ttest_ind
https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_ind.html

