二項分布とは何か？期待値、分散、例

【目次】

二項分布とその確率質量関数、期待値、分散
二項分布の例
ベルヌーイ分布と二項分布の関係
二項分布を正規分布で近似する。
練習問題
練習問題回答

二項分布とその確率質量関数、期待値、分散

二項分布(Binomial distribution)は二択の結果（「成功」と「失敗」など）が出る試行を一定数繰り返し、そのうち何回「成功」の結果が得られるかの確率を表す離散型確率分布です。

このときの毎回の試行において「成功」が得られる確率をp、「失敗」が得られる確率を1-pと表し、「成功確率」pは毎回等しいものとします。また、同じ試行を繰り返す回数を通常nで表します。

確率変数Xが試行回数n、成功確率pの二項分布に従うことを、

$X\sim Binomial(n,p)$ 又は $X\sim B(n,p)$

などと表します。

この確率分布の確率質量関数、期待値、分散は以下の通りです。

二項分布の確率質量関数、期待値E(X)、分散Var(X)

•確率質量関数
$f_{X}(x)=\displaystyle{{}_n C_{x}\cdot p^{x}\cdot(1-p)^{n-x}} \qquad (x=0,1,2,\cdots,n)$

•期待値
$E(X)=np$

•分散
$Var(X)=np(1-p)$

なお、 ${}_n C_{x}$ はn個の中からx個を選ぶ時、何通りの選び方があるか？を表します。高校数学Aで学習する「組み合わせ」という概念ですので、これが分からない方は、復習されることをお勧めします。

それでは例を見てみましょう。

二項分布の例

歪んだコインがあり、このコインを投げると表が出る確率を0.6とし、裏が出る確率を0.4とします。このコインを２回投げたとき、表が出る回数を確率変数Xとすると、Xはn=2、p=0.6の二項分布に従います。

つまり、 $X\sim Bonimial(2,0.6)$ となります。

このコインを2回投げて0回表が出る確率、つまりP(X=0)、1回だけ表が出る確率、つまりP(X=1)、そして2回とも表が出る確率、P(X=2)を二項分布の確率質量関数を用いて計算してみます。

まず、この分布の確率分布は以下のように表すことができますね。

•確率質量関数(pmf)

$f_{X}(x)=P(X=x)=\displaystyle{{}_2 C_{x}\cdot 0.6^{x}\cdot 0.4^{2-x}} \qquad (x=0,1,2)$

•0回表が出る確率

$f_{X}(0)=P(X=0)=\displaystyle{{}_2 C_{0}\cdot 0.6^{0}\cdot 0.4^{2}}=1\cdot 1\cdot 0.16 = 0.16$

•1回だけ表が出る確率

$f_{X}(1)=P(X=1)=\displaystyle{{}_2 C_{1}\cdot 0.6^{1}\cdot 0.4^{1}}=2\cdot 0.6\cdot 0.4 = 0.48$

•2回とも表が出る確率

$f_{X}(2)=P(X=2)=\displaystyle{{}_2 C_{2}\cdot 0.6^{2}\cdot 0.4^{0}}=1\cdot 0.36\cdot 1 = 0.36$

確率分布表

表の回数(X)	確率
0	0.16
1	0.48
2	0.36
それ以外	0

•期待値
$E(X)=np=2\cdot 0.6=1.2$

•分散
$Var(X)=np(1-p)=2\cdot 0.6\cdot 0.4=0.48$

また、上記の結果を用いて、例えばこのコインを２回投げて、１回以上表が出る確率、つまりP(X=1 又は 2)を求めたいとき、

$P(X=1,2)=P(X=1)+P(X=2)=0.48+0.36=0.84$

というように求めることができます。

ベルヌーイ分布と二項分布の関係

「ベルヌーイ分布とは何か？」のページで学習したベルヌーイ分布と二項分布の関係を見ていきます。

ベルヌーイ分布と二項分布の関係

n個の確率変数 $X_{1},X_{2},\cdots,X_{n}$ が独立であり、それぞれ成功確率pのベルヌーイ分布に従う時、このn個の確率変数の和は試行回数n、成功確率pの二項分布に従います。

つまり、

$X_{1},X_{2},\cdots,X_{n}$ が独立で、

$X_{i}\sim Bernoulli(p) \qquad (i=1,2,\cdots,n)$

のとき、Xを確率変数

$X=\Sigma^n_{i=1}X_i=X_{1}+X_{2}+\cdots+X_{n}$

とすると、

$X=\Sigma^n_{i=1}X_i\sim Binomial(n,p)$

となります。

例

前述の表が出る確率がp=0.6のコインを考えてみましょう。

$X_1$ を１回目にコインを投げて表がでたら1、裏がでたら0の確率変数とします。

$X_2$ を2回目にコインを投げて表がでたら1、裏がでたら0の確率変数とします。

この確率変数 $X_1, X_2$ はどちらも成功確率p=0.6のベルヌーイ分布に従いますね。

そして、1回目コインの結果（表、裏）が2回目にコインを投げた時の結果に影響を与えることはないので、 $X_1$ と $X_2$ は独立した確率変数です。

ですので、この二つの確率変数の和 $X_1+X_2$ は試行回数n=2,p=0.6の二項分布に従います。

つまり、

$X_1+X_2\sim Binomial(2,0.6)$

となります。

二項分布を正規分布で近似する。

さて、二択の試行を繰り返し行うときに何回「成功」が得られるかを考えるのに便利な二項分布ですが、試行回数nが十分に大きい場合、二項分布を正規分布で近似的に表すことができます。

「正規分布とは何か？」のページで詳しく説明しますが、正規分布はよく見る左右対称のベル型の分布のことです。

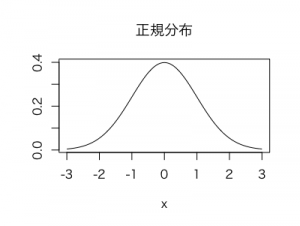
なぜわざわざ二項分布を正規分布で近似的に表す必要があるのでしょうか？

例えば、前述の表が出る確率がp=0.6の偏ったコインを1000回投げて、表が出る回数が500回以上600回以下になる確率、つまり $P(500\leq X\leq 600)$ を求めたい時、

二項分布を利用してP(X=500)+P(X=501)+・・・+P(X=600)と101項を足し合わせて計算することができますが、電卓を叩いてこれを足し合わせるのは非常に面倒です。

そのため、この二項分布を正規分布で近似的に表して、正規分布の確率密度関数をXが500から600の範囲で積分することにより、この確率を求めることができるので便利なケースがあるのです。

ということで、以下が二項分布と正規分布の関係です。

二項分布を正規分布で近似的に表す。

確率変数Xが試行回数n、成功確率pの二項分布に従うとき、

つまり、 $X\sim Binomial(n,p)$ のとき、

nが十分に大きければ、この分布を

平均値 $\mu=np$ 、分散 $\sigma^2=np(1-p)$ の正規分布、

つまり $Normal(np,np(1-p))$ で近似することができる。

実際に表が出る確率（成功確率）p=0.6のコインを投げる例を見てみましょう。

まず、例えばこのコインを2回だけ投げたときの表が出る数の分布は、以下の図のようになりますね。

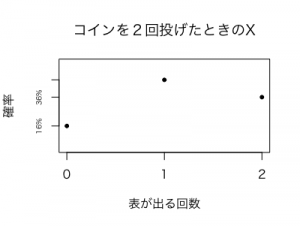
このグラフでは、何となくベル型の分布には見えますが、左右対称とは言えませんね。

次にn=5、n=10とコインを投げる回数を増やしていって、表が出る確率の分布を見てみます。

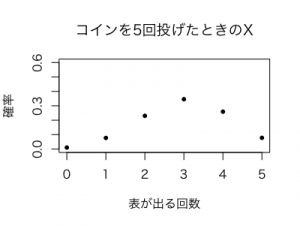
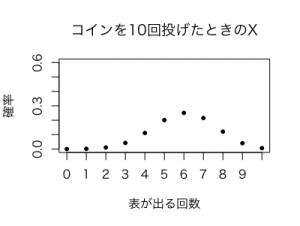
ベル型の正規分布っぽくなってきてはいますが、まだ左側に裾をひいたような形のグラフになっています。

そして、コインを投げる回数nを1000回まで増やすと、以下のようなグラフになります。

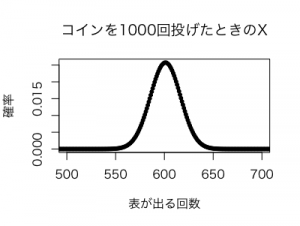
ほぼ完全にベル型の左右対称のグラフ、つまり正規分布の確率密度関数のグラフになりました。

この正規分布の平均値と分散は上記の公式で計算できますから、Xは近似的に

•平均値μ=np=1000•0.6=600
•分散σ²=np=1000•0.6•0.4=240

の正規分布に従うといえます。

以下に、平均値600、分散240の正規分布の確率密度関数のグラフを赤で重ねてみます。

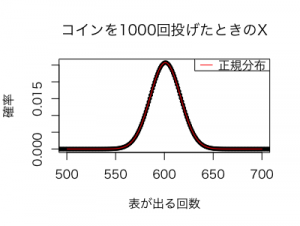
見事に正規分布とほぼ同じになっていますね。
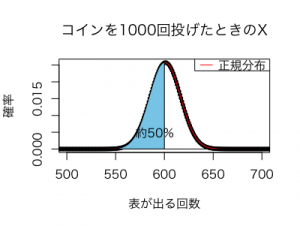
そして、この近似的に表した正規分布を利用して、 $500\leq X\leq 600$ となる確率は、以下の図の青く塗られた部分なので、この確率は約50%、つまり、 $P(500 \leq X\leq 600)\approx 0.5$ となることが分かります。