F分布とは何か？確率密度関数、期待値、分散、F検定。

【目次】

F分布の定義と例
F分布のグラフ
F分布の確率密度関数、期待値、分散
F分布を使った検定
練習問題
練習問題回答

F分布の定義と例

F分布(F distribution)とは、等分散の検定や、重回帰分析におけるパラメーターの検定などの統計学的検定に利用される分布で、２つの自由度によって形が決まる分布です。

F分布の定義は以下のようになります。

F分布の定義

確率変数U,Vが独立で、それぞれに自由度p,qのカイ二乗分布に従うとき、確率変数 $X=(U/p)/(V/q)$ は自由度p,qのF分布に従う。

つまり、 $U\sim \chi^2_{p}$ , $V\sim \chi^2_{q}$ , $U{\perp\!\!\!\perp} V$ のとき、

$X=\dfrac{U/p}{V/q}\sim F_{p,q}$

となる。

例を見てみましょう。UがVがお互いに独立で、それぞれ自由度３、自由度30のカイ二乗分布に従うとします。

すると、 $X=(U/3)/(V/30)\sim F_{3,30}$ となります。

実際にシュミレーションをして確かめて見ましょう。

Rを使って、Uを自由度３のカイ二乗分布、Vを自由度30のカイ二乗分から抽出し、 $X=(U/3)/(V/30)$ を計算してみます。

set.seed(10)
# 自由度３のカイ二乗分布から抽出
U=rchisq(1,3)
# 自由度30のカイ二乗分布から抽出
V=rchisq(1,30)
# Xを計算
X=(U/3)/(V/30)

> round(X,3)
[1] 0.738

$X_{1}=0.783$ が抽出されました。これを1000回ほど繰り返して、 $X_{1},\cdots,X_{1000}$ がどのような分布を描くか、確認してみます。

以下がそのヒストグラムです。

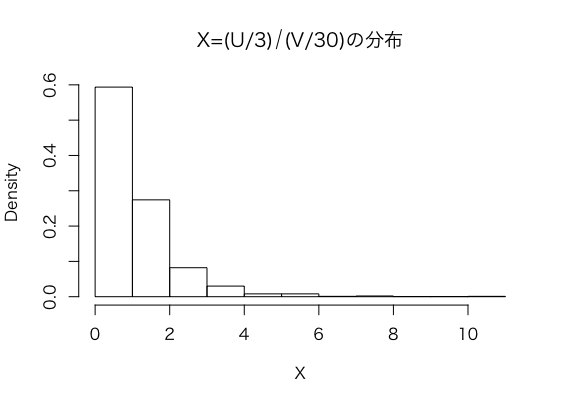
このヒストグラムに、自由度3,30のF分布の確率密度関数を重ねると以下のようになります。

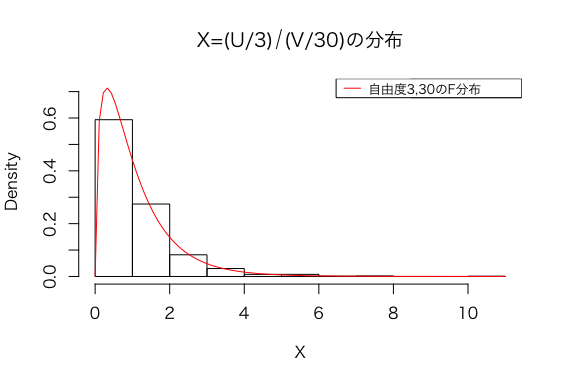
シュミレーションで抽出された $X_1,\cdots,X_{1000}$ が見事に自由度3,30のF分布に従っているのが確認できます。

F分布のグラフ

F分布のグラフは、2つの自由度と呼ばれるパラメータによって形が決まります。

また、前述のF分布の定義におけるパラメータpを固定し、qを無限大に近づけていくとF分布は自由度pのカイ二乗分布に従います。

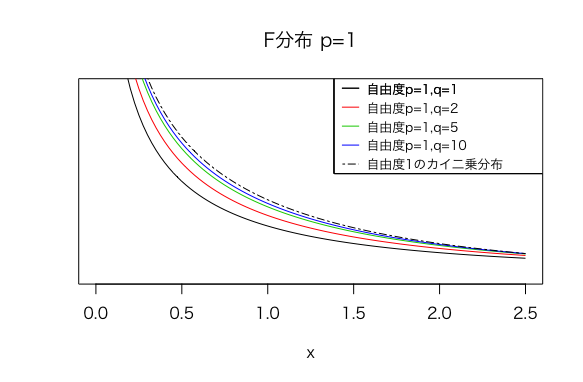
上のように、p=1を固定して、qを大きくしていくと、自由度１のカイ二乗分布になることが分かりますね。

以下は、q=1を固定してpを大きくしていった場合のF分布のグラフです。

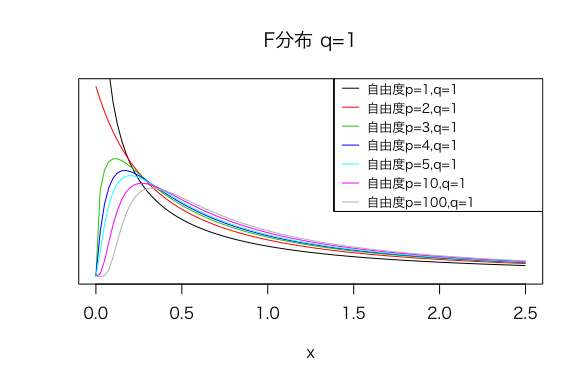
以下は、p,qを両方とも大きくしていった場合のグラフです。

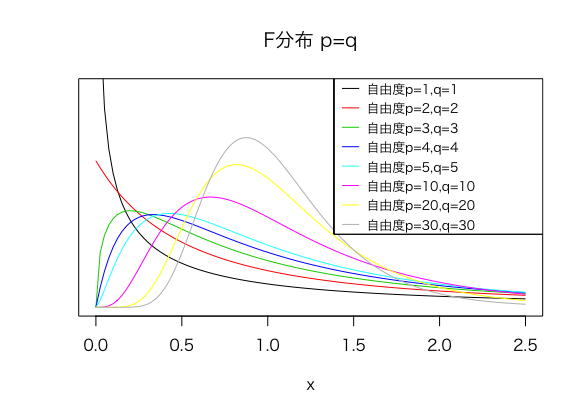
このようにF分布は主に、右に歪んだ形になりますが、パラメータによって多少形が変わってくることが分かります。

F分布の確率密度関数、期待値、分散

F分布の確率密度関数、期待値、分散

Xが自由度p,qのF分布に従う時、つまり、 $X\sim F_{p,q}$ のとき:

・確率密度関数

$f_{X}(x)=\dfrac{\Gamma(\frac{p+q}{2})}{\Gamma(\frac{p}{2})\Gamma(\frac{q}{2})}\bigg(\dfrac{p}{q}\bigg)^{p/2}\dfrac{x^{(p-2)/2}}{(1+\frac{p}{q}x)^{(p+q)/2}} \qquad(0\le x\textless \infty); p,q=1,2,3,\cdots$

※ $\Gamma(n)=(n-1)!$

・期待値
$E(X)=\frac{q}{q-2}\qquad 2\textless q$
・分散
$Var(X)=2(\frac{q}{q-2})^2\dfrac{(p+q-2)}{p(q-4)}\qquad 4\textless q$

F分布を使った検定

F分布は等分散性の検定や、重回帰分析のパラメータの検定など、幅広く統計検定に利用されます。詳しくは「統計学の基礎」や、各検定手法を取り扱う項目にて解説します。

F検定というと、すなわち、等分散性の検定のことをいうと勘違いをしている人が多いですが、検定統計量がF分布に従う検定を総称してF検定と呼びます。

練習問題

互いに独立な確率変数X,Yがそれぞれ、自由度3,4のカイ二乗分布に従う時、確率変数 $(X/3)/(Y/4)$ はどんな確率分布に従うか？

練習問題解答

確率変数 $(X/3)/(Y/4)$ は自由度3,4のF分布に従う。つまり、

$(X/3)/(Y/4)\sim F_{3,4}$

MENU

F分布の定義と例

F分布のグラフ

F分布の確率密度関数、期待値、分散

F分布を使った検定

練習問題

練習問題解答

確率分布

スポンサー募集中。

更新・勉強会などの情報を受け取る。

理系の就職・職業訓練