一様分布について
一様分布(Uniform distribution)とは確率変数Xが取り得る範囲ですべての実現値が得られる確率が等しい分布です。
一様分布には離散型一様分布と、連続型一様分布がありますので、別々に見ていきましょう。
離散型一様分布
離散型確率変数Xが離散型一様分布(Discrete uniform distribution)に従う時、Xの取り得る値(実現値)の最小値をa、最大値をbとすると、Xは{a,a+1,a+2,···,b-2,b-1,b}の各値を等しい確率でとります。
つまり、実現値は全部でb-a+1個あるため、Xが各実現値を取り得る確率は1/(b-a+1)となります。
このように最小値がa,最大値がbをとる離散型一様分布を
などと表し、確率変数XがUniform{a,b}に従うことを、
などと表記します。
この関数の確率質量関数は以下の通りです。
また離散型一様分布に従う確率変数Xの期待値E(X)と分散Var(X)は以下の公式で得られます。
離散型確率変数
•期待値
•分散
離散型一様分布の例
さてさて、確率論の勉強を始めると頻繁に目にする例、サイコロを1回振って出た目を確率変数Xとすると、Xはまさに離散型の一様分布に従います。
Xが取り得る実現値は{1,2,3,4,5,6}ですから、上述の公式の中では最小値a=1、最大値はb=6ですね。
そして確率質量関数を公式で求めると
となります。
常識的に考えて、サイコロが歪んでいない場合、どの目が出る確率も以下の表のように同じ1/6ですから、この確率質量関数には納得がいくのではないでしょうか。
確率分布表
| 出る目 | 確率 |
| 1 | 1/6 |
| 2 | 1/6 |
| 3 | 1/6 |
| 4 | 1/6 |
| 5 | 1/6 |
| 6 | 1/6 |
| それ以外 | 0 |
この関数のグラフを描くと以下のようになりますね。
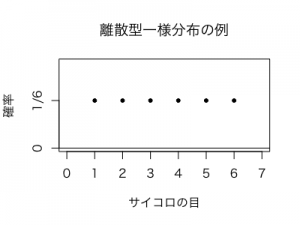
次に期待値と分散も公式を利用して求めましょう。
•期待値
•分散
期待値は3.5、分散は約2.92と求めることができました。この分散2.92は「分散、又は標準偏差とは何か?」のページでは分散の定義を用いてサイコロの目の分散を計算していますが、しっかりと値が一致していることが分かります。
連続型一様分布
連続型確率変数Xが連続型一様分布(Continuous uniform distribution)に従う時、a1,a2,b1,b2がすべてXの取り得る範囲内にあるとき、Xが[a1,b1](a1以上b1以下)の値をとる確率と、[a2,b2](a2以上b2以下)の値をとる確率は、それぞれの区間の長さが同じ場合、等しくなります。
つまり、b1-a1=b2-a2のとき、となります。
なぜこのようなややこしい言い方になるかというと、Xが連続型確率変数のとき、Xがある1点(X=a, X=10など)をとる確率は理論的に0であるため、区間で考える必要があるからです。
(「連続型確率変数と離散型確率変数の違いとは?」参照。)
表記は連続型確率変数Xがaからbまでの値をとる連続型一様分布を
と表し、確率変数XがUnif(a,b)に従うことを、
などと表記します。
この連続型一様分布の確率密度関数(pdf)は以下の通りです。
連続型一様分布に従う確率変数Xの期待値E(X)と分散Var(X)は以下の公式で得られます。
連続型確率変数
•期待値
•分散
言葉で正確に説明しようとすると多少わかりにくいですが、例を見れば簡単に理解しやすいと思いますので、早速例を見てみましょう。
連続型一様分布の例
確率変数Xが0から10の間の値を取り得る連続型一様分布に従うとすると以下のように表記します。
この分布の確率密度関数は
となり、これをグラフを描くと以下のようになります。
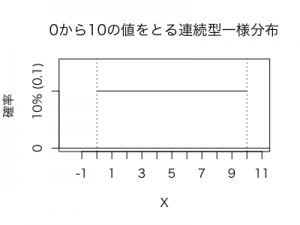
例えば以下のように1〜3の区間は長さが2、6〜8の区間も長さが2で同じなのでXが[1,3]の値をとる確率と、[6,8]の値をとる確率はともに20%(0.2)で同じになりますね。
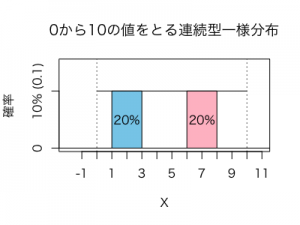
この分布の期待値E(X)は
分散Var(X)は
と計算できます。
練習問題
サイコロを1回振って出る目を離散型確率確率変数Xとします。さて、別の確率変数YをY=X+1とすると、Yはどんな確率分布に従うか?また、その確率質量関数と、Yの期待値、分散を求めましょう。
練習問題回答
Yは{2,3,4,5,6,7}の値をとる離散型一様分布に従います。つまり、
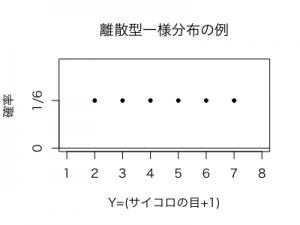
確率質量関数
期待値
分散
「離散型一様分布の例」ではXの期待値E(X)=3.5、分散Var(X)=2.92と計算結果がでましたが、Y=X+1とすると、Yの期待値はXより丁度1大きくなり、Yの分散はXと同じ約2.92となります。

