ポアソン分布とは何か？期待値、分散、例

【目次】

ポアソン分布とその確率質量関数、期待値、分散
ポアソン分布の例
二項分布とポアソン分布の関係
練習問題
練習問題回答

ポアソン分布とその確率質量関数、期待値、分散

ポアソン分布(Poisson distribution)は、一定時間にある出来事が起こる回数など、回数、頻度、個数などを説明する際に利用される離散型の確率分布です。

例えば、

•ある種の魚が１回の産卵で産む卵の数。
•1日にあなたが受け取るメールの数。
•夜中10時から12時の間にある病院の集中治療室に運ばれる人の人数。

などを確率変数として、この確率変数が0以上の整数の値をとるような場合、ポアソン分布を用いて説明できることがあります。

ポアソン分布のパラメータはλ(ラムダ)と表すことが多く、λは0より大きい正の値をとります。つまり、λ>0。

ポアソン分布では期待値と分散がパラメータλと等しくなります。

確率変数Xがパラメータλのポアソン分布に従うことを、

$X\sim Pois(\lambda)$

などと表します。

ポアソン分布の確率質量関数(pmf)、期待値、分散は以下の通りです。

ポアソン分布の確率質量関数、期待値E(X)、分散Var(X)

確率変数Xがパラメータλのポアソン分布に従う時、つまり、

$X\sim Pois(\lambda)$

のとき、

•確率質量関数
$f_{X}(x)=P(X=x)=\displaystyle{\frac{\lambda^x e^{-\lambda}}{x!}}\qquad (x=0,1,2,\cdots)$

※eはネイピア数と呼ばれ約2.718のことです。
※x!とはx階乗（かいじょう）と読み、x以下の整数をすべて掛け合わせることです。
（例えば $4!=4\times 3\times 2\times 1=24$ ）

•期待値
$E(X)=\lambda$

•分散
$Var(X)=\lambda$

ポアソン分布の例

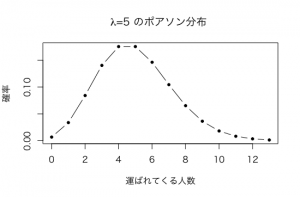
ある病院で夜中の12時から1時の1時間の間に緊急治療室に運ばれてくる患者さんの人数を確率変数Xとすると、Xはパラメータλ=5のポアソン分布に従うとします。

つまり、 $X\sim Pois(5)$

この確率変数Xの確率質量関数、期待値、分散を求めてみましょう。

そして、その確率質量関数を資料して、

•その1時間内に1人も患者さんが運ばれてこない確率
•1人しか患者さんが運ばれてこない確率
•2人患者さんが運ばれてくる確率

などを求めてみます。

まず、確率質量関数、期待値、分散は以下の通り。

•確率質量関数
$f_{X}(x)=P(X=x)=\displaystyle{\frac{5^x e^{-5}}{x!}}\qquad (x=0,1,2,\cdots)$

•期待値
$E(X)=\lambda$

•分散
$Var(X)=\lambda$

上記の確率質量関数を利用して、患者さんが1人も運ばれてこない確率、つまり、X=0の確率は

$P(X=0)=f_{X}(0)=\displaystyle{\frac{5^0 e^{-5}}{0!}}\approx \frac{1\cdot2.718^{-5}}{1}\approx 0.0067$

となり、約0.67%と非常に小さい確率ですね。

なお、0!（ゼロの階乗）は0!=1と定義されます。感覚的には納得いきませんが、このように数学的に定義されていますので、単純に「ゼロの階乗は１」と覚えましょう。

次に患者さんが1人だけ運ばれてくる確率です。

$P(X=1)=f_{X}(1)=\displaystyle{\frac{5^1 e^{-5}}{1!}}\approx \frac{5\cdot2.718^{-5}}{1}\approx 0.034$

そして患者さんが2人運ばれてくる確率:

$P(X=2)=f_{X}(2)=\displaystyle{\frac{5^2 e^{-5}}{2!}}\approx \frac{25\cdot2.718^{-5}}{2}\approx 0.084$

このように確率質量関数を利用してP(X=3),P(X=4),•••を求めると、以下の確率分布表のようになりますね。

確率分布表

X:人数	確率
0	0.7%
1	3.4%
2	8.4%
3	14.0%
4	17.5%
5	17.5%
6	14.6%
7	10.4%
8	6.5%
9	3.6%
10	1.8%
11	0.8%
12	0.3%
13以上	0.1%

二項分布とポアソン分布の関係

次に二項分布とポアソン分布の関係を見ていきます。

二項分布は「二項分布とは何か？」のページで学習した通り、成功確率pで「成功」、失敗確率1-pで「失敗」の二択の結果が得られる試行をn回繰り返した時、何回「成功」が得られるか？の確率分布ですね。

この二項分布の $n\times p$ を一定の値に保ったまま、nを限りなく大きくしていき、同時にpを限りなく小さくしていくと、パラメータ $\lambda=np$ のポアソン分布になります。

例:二項分布がポアソン分布に収束する。

上記の例では、パラメータλ=5のポアソン分布を見ましたが、試行回数n、成功確率がpの二項分布をnp=5に保って、nを大きく、pを小さくしていくとどうなるかを観察してみます。

まずはn=6,p=5/6の例を考えてみます。

n=6ですので、１時間を6つに分けると、毎10分ごとに、p=5/6の確率で患者さんが運ばれてくる二項分布と考えることができます。

$X\sim Binomial(6,5/6)$ をグラフで表すと以下のようになります。

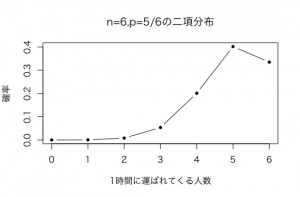
λ=5のポアソン分布とは似ても似つきません。

次にn=60, p=5/60=1/12までnを大きくしてpを小さくしてみましょう。

つまり、1時間をn=60の期間に分けていますから、1分毎にp=1/12の確率で患者さんが運ばれてくる二項分布ということになります。

$X\sim Binomial(60,1/12)$ のグラフは以下のようになります。

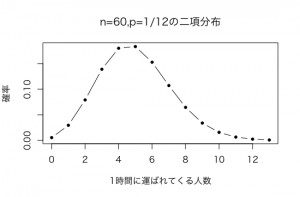
かなりλ=5のポアソン分布に近づいてきました。

そして、次にn=3600,p=5/3600の二項分布を見てみます。

つまり、1秒毎に患者さんが運ばれてくる確率がp=5/3600の二項分布です。

$X\sim Binomial(3600,5/3600)$ のグラフは以下の通り。

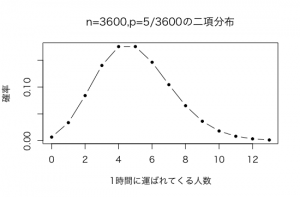
パラメータλ=5のポアソン分布と全くといってよいほど同じになっています。

このように、二項分布の $n\times p$ を一定の値に保ったまま、nを大きくしていき、pを小さくしていくと、 $\lambda=np$ をパラメータとするポアソン分布に収束します。

練習問題

ある小さなオフィスで1時間に電話がなる回数を確率変数Xとすると、Xは期待値E(X)=6、分散Var(X)=6のポアソン分布に従うとします。このオフィスで1時間に電話がなる回数が3回となる確率を、ポアソン分布の確率質量関数を用いて求めてみましょう。

練習問題回答

ポアソン分布においては、期待値E(X)=分散Var(X)=パラメータλとなるので、このポアソン分布のパラメータはλ=6となります。つまり、

$X\sim Poisson(6)$

このポアソン分布の確率質量関数は

$f_{X}(x)=\displaystyle{\frac{6^x e^{-6}}{x!}} \qquad (x=0,1,2,\cdots)$

電話が1時間に3回かかってくる確率は

$P(X=3)=f_{X}(3)=\displaystyle{\frac{6^3 e^{-6}}{3!}}\approx \displaystyle{\frac{6^3\cdot 2.718^{-6}}{3!}}=0.089$

なので、約8.9%となります。

MENU

ポアソン分布とその確率質量関数、期待値、分散

ポアソン分布の例

二項分布とポアソン分布の関係

例:二項分布がポアソン分布に収束する。

練習問題

練習問題回答

確率分布

スポンサー募集中。

更新・勉強会などの情報を受け取る。

理系の就職・職業訓練