社会人が統計学の基礎を学び、実務で活かす

MENU

正規分布とは何か？期待値、分散、例

HOME »
確率分布 »
正規分布とは何か？期待値、分散、例

【目次】

正規分布とその確率密度関数、期待値、分散
正規分布の例
68%,95%,99.7%の法則
練習問題
練習問題回答

正規分布とその確率密度関数、期待値、分散

正規分布(Normal distribution)とは統計学において最もよく利用される平均値を中心にしてベル型の左右対称の連続型確率分布で、分布の形は2つのパラメータである平均値μと分散σ²によって決まります。

ちなみにμは「ミュー」、σは「シグマ」と読みます。

正規分布は別名ガウス分布(Gaussian distribution)と呼ばれます。

平均値μは分布のベル型の中心がどこになるかを決定し、分散σ²は分布が左右にどれだけ幅広く広がっていくかを決定します。

確率変数Xが平均値μ、分散σ²の正規分布に従うことを

$X\sim Normal(\mu,\sigma^2)$ 又は $X\sim N(\mu,\sigma^2)$

などと表します。

正規分布の確率密度関数(pdf)、期待値、分散は以下の通りです。

正規分布の確率密度関数、期待値E(X)、分散Var(X)

確率変数Xが平均値μ、分散σ²の正規分布に従う時、つまり、

$X\sim N(\mu,\sigma^2)$

のとき、

•確率密度関数
$f_{X}(x)=\displaystyle{\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}}$ 又は $f_{X}(x)=\displaystyle{\frac{1}{\sqrt{2\pi}\cdot\sigma}exp\big(-\frac{(x-\mu)^2}{2\sigma^2}}\big)$ (-∞<x<∞)

※eはネイピア数と呼ばれ約2.718のことです。
※exp(x)はeのx乗の意味です。
※上記２つの式は全く同じことを違う表記を用いて表しただけです。
※-∞<x<∞とは、xがマイナス無限大からプラス無限大までのすべての実数を取り得る、という意味です。

•期待値
$E(X)=\mu$

•分散
$Var(X)=\sigma^2$

正規分布の例

同質性の高い集団における各人の身長はおおよそ正規分布に従うと言われています。

仮に、日本人成人男性をランダムに一人抽出した時のその人の身長を確率変数Xとすると、Xが平均μ=171cm、分散σ²=64の正規分布に従うとします。
(これは筆者の肌感覚で大体正しいと思われるものです。正式なデータではありません。)

なお分散がσ²=64なので、標準偏差はσ=8となりますね。

この場合 $X\sim N(171,64)$ と表すことができます。

この確率分布の、確率密度関数、期待値E(X)、分散Var(X)を見ていきます。

•確率密度関数
$f_{X}(x)=\displaystyle{\frac{1}{\sqrt{2\pi}\times 8}e^{-\frac{(x-171)^2}{2\times 8^2}}}=\displaystyle{\frac{1}{8\sqrt{2\pi}}e^{-\frac{(x-171)^2}{128}}}$

•期待値
E(X)=μ=171

•分散
Var(X)=σ²=64

となります。正規分布の期待値と分散は、パラメータ(μ,σ²)そのものですね。

68%,95%,99.7%の法則

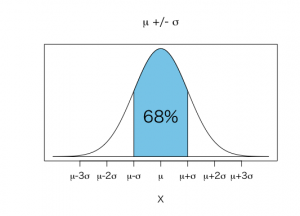
正規分布では平均値μから左右に±1標準偏差(σ)内に68%、±2標準偏差(σ)内に95%、±3標準偏差(σ)内に99.7%の確率で事象が発生します。

範囲	確率
μ±σ	68%
μ±2σ	95%
μ±3σ	99.7%

図で表すと以下のようになりますね。

平均値±1標準偏差に68%
rplot1

rplot1

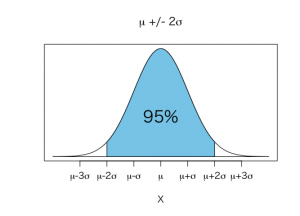
平均値±2標準偏差に95%
rplot2

rplot2

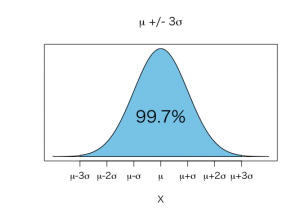
平均値±3標準偏差に99.7%
rplot3

rplot3

例

それでは68%,95%,99.7%の法則の例を見てみましょう。

前述のように、日本人成人男性をランダムに一人選んだとき、その人の身長を確率変数Xとすると、確率変数Xが平均値μ=171,分散σ²=64(つまり標準偏差σ＝8)の正規分布に従うと仮定します。

平均値から前後1標準偏差は163から179ですから、日本人の成人男性全体の68%が163cm以上179cm以下の身長になるとわかります。

また、日本人成人男性を一人ランダムに抽出したとき、その人の身長が163cm以上179cm以下である確率は $P(163\leq X\leq 179)=68\%$ ということができます。

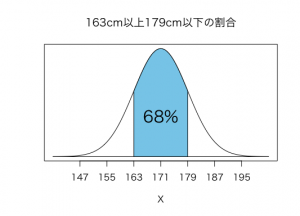
rplot4

なお、この正規分布の曲線は、先ほどの例で求めた

$f_{X}(x)=\displaystyle{\frac{1}{8\sqrt{2\pi}}e^{-\frac{(x-171)^2}{128}}}$

のグラフです。そしてこの確率密度関数を163から179で積分すると、

$\displaystyle{\int_{163}^{179}\frac{1}{8\sqrt{2\pi}}e^{-\frac{(x-171)^2}{128}}}dx\approx 0.683$

となり、約68%となります。

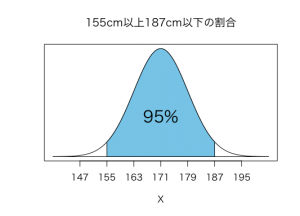
次に平均値から前後2標準偏差は155から187ですから、日本人の成人男性全体の95%が155cm以上187cm以下の身長になるとわかります。

また、日本人成人男性を一人ランダムに抽出したとき、その人の身長が155cm以上187cm以下である確率は $P(155\leq X\leq 187)=95\%$ ということができます。

rplot5

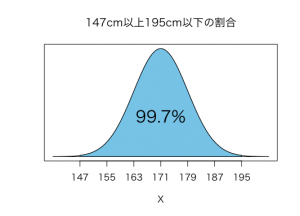
そして平均値から前後3標準偏差は147から195ですから、日本人の成人男性全体の99.7%が147cm以上195cm以下の身長になるとわかります。

また、日本人成人男性を一人ランダムに抽出したとき、その人の身長が155cm以上187cm以下である確率は $P(147\leq X\leq 195)=99.7\%$ ということができます。

rplot6

練習問題

例と同じように、日本人成人男性の身長が平均値179、標準偏差8の正規分布に従うと仮定します。

（１）身長171cm以上179cm以下の人は全体の何パーセントでしょうか？
（２）身長155cm以下または187cm以上の人は全体の何パーセントでしょうか？

練習問題回答

正規分布は左右対称なので、68%,95%,99.7%の法則を用いて以下の図の色が付いている部分を求めることができます。

（１）身長171cm以上179cm以下の人

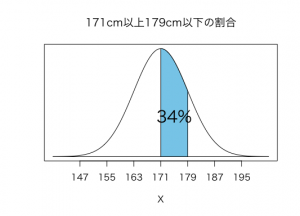
rplot7

身長171cm以上179cm以下は平均値171から、１標準偏差分大きい179までの範囲ですから34%と求めることができます。

（２）身長155cm以下または187cm以上の人

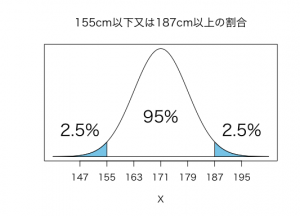
rplot8

身長155cm以上187cm以下は平均値171から±2標準偏差分ですから、95%、そして正規分布は左右対称ですから、その範囲の外は左右各2.5%です。ですので、身長155cm以下または187cm以上の人は全体の5%と求められます。

確率分布

PAGETOP

Copyright © 【統計学の入門サイト】統計ドットリンク All Rights Reserved.

Powered by WordPress & BizVektor Theme by Vektor,Inc. technology.