標準正規分布とは何か？正規分布と標準化

【目次】

標準正規分布とその確率密度関数、期待値、分散
正規分布の標準化
正規分布を標準化する利点
練習問題
練習問題回答

標準正規分布とその確率密度関数、期待値、分散

標準正規分布とは、平均値0、分散1の正規分布のことです。

標準偏差は分散の平方根をとったものですから、標準正規分布においては標準偏差σ=分散σ²=1 となります。

確率変数Zが標準正規分布に従うことを

$Z\sim N(0,1)$

などと表します。標準正規分布に従う確率変数は慣例的にZを用いて表記することが多いですが、別にXでもYでもUでも何でも構いません。

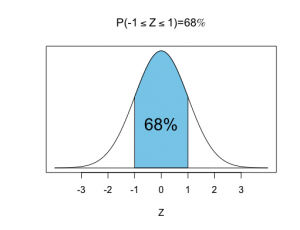
•68%-95%-99.7%の法則

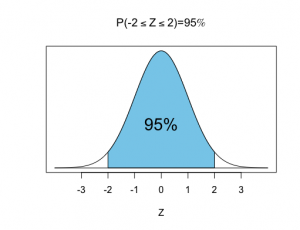
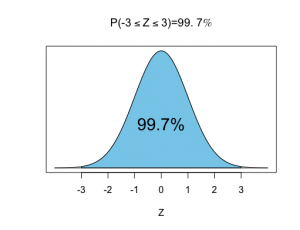
Zが標準正規分布に従うとき、 $-1\leq Z\leq 1$ となる確率は68%、 $-2\leq Z\leq 2$ となる確率は95%、 $-3\leq Z\leq 3$ となる確率は99.7%となります。

標準正規分布の確率密度関数(pdf)、期待値、分散は以下の通りです。

標準正規分布の確率密度関数、期待値E(X)、分散Var(X)

確率変数Zが標準正規分布に従う時、つまり、

$Z\sim N(0,1)$

のとき、

•確率密度関数
$f_{X}(x)=\displaystyle{\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}}\quad$ 又は $\quad f_{X}(x)=\displaystyle{\frac{1}{\sqrt{2\pi}}exp\big(-\frac{x^2}{2}}\big)$ (-∞<x<∞)

※eはネイピア数と呼ばれ約2.718のことです。
※exp(x)はeのx乗の意味です。
※上記２つの式は全く同じことを違う表記を用いて表しただけです。
※-∞<x<∞とは、xがマイナス無限大からプラス無限大までのすべての実数を取り得る、という意味です。
※この確率密度関数は単純に平均値μ、分散σ²の正規分布の確率密度関数に、μ=0、σ=1を代入したものです。

•期待値
$E(X)=0$

•分散
$Var(X)=1$

正規分布の標準化

正規分布に従う確率変数Xから少し加工することによって、この確率変数を標準正規分布に従う確率変数に変換することができます。

正規分布の標準化

確率変数Xが平均値μ、分散σ²の正規分布に従う時、つまり

$X\sim N(\mu,\sigma^2)$

のとき、Zを以下のように定義する。

$Z=\displaystyle{\frac{X-\mu}{\sigma}}$

すると、Zは標準正規分布に従う。つまり、

$Z=\displaystyle{\frac{X-\mu}{\sigma}}\sim N(0,1)$

となる。

例

「正規分布とは何か？」のページで例に挙げたように、日本人成人男性をランダムに抽出したときにその人の身長をXとすると、Xが平均値μ=171、σ²=64の正規分布に従うと仮定します。つまり、

$X\sim N(171,64)$

とすると、標準偏差は $\sigma=\sqrt{64}=8$ なので、 $Z=\displaystyle{\frac{X-171}{8}}$ は標準正規分布に従います。つまり、

$Z=\displaystyle{\frac{X-171}{8}}\sim N(0,1)$

となります。

実際に統計解析プログラム言語のRを利用して、試してみましょう。
(Rに関しては「プログラミングとソフトウェア」のページでサンプルコードなどを公開しています。)

まずは、Rのrnorm()という関数を利用して、平均値171、標準偏差8の正規分布から100個のデータを抽出してみます。
Rコードはrnorm(100,171,8)となります。

[1] 171.8773 175.2360 161.4433 183.5854 176.2689 167.3399 168.9672 169.2207
[9] 171.9644 174.5393 167.0860 166.8736 176.7758 166.9547 190.9706 185.0018
[17] 178.8762 154.1994 180.3071 156.2226 179.2115 171.2995 180.1582 174.1045
[25] 178.0964 152.9600 180.8156 179.0257 171.6139 163.0513 172.6547 175.5997
[33] 166.2158 164.3318 162.3599 172.0817 156.3943 156.7550 172.9781 164.6527
[41] 172.7019 180.3144 165.1980 172.9449 161.9903 160.0263 169.4561 175.2113
[49] 168.0864 183.2570 171.3925 176.0706 156.3735 163.7605 180.2097 172.7211
[57] 170.9525 172.3925 182.1086 178.0820 165.3806 162.8325 161.6839 179.4556
[65] 171.7212 170.0898 166.3461 166.6954 162.9575 172.8633 164.4242 160.3757
[73] 185.6517 175.1032 178.8395 172.0364 162.5324 159.9103 173.3461 170.3930
[81] 163.5008 180.3340 153.7431 166.7406 168.1200 175.0183 163.8822 173.6402
[89] 181.4257 182.9208 176.2215 165.3290 173.3727 164.7621 162.8859 157.7915
[97] 174.3279 174.5383 171.7994 165.7310

このように100個のデータを抽出することができました。このデータのヒストグラムを作成し、分布を見てみると以下のようになります。

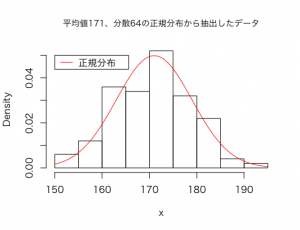
さて、それでは変数変換をしてこの抽出したデータが標準正規分布に従うように加工しましょう！

そのために、上記で羅列した100個のデータ一つ一つから、平均値である171を引いて、標準偏差8で割る、ということをします。

つまり、最初のデータが $x_1=171.8773$ ですから、 $\displaystyle{\frac{171.8773-171}{8}=0.10966}$ 、

２個目のデータが $x_2=175.2360$ ですから、 $\displaystyle{\frac{175.2360-171}{8}=0.5295}$ 、

というように100個全部を標準化すると、以下の100個のデータが得られます。

[1] 0.109662975 0.529495248 -1.194590518 1.573174266 0.658614246
[6] -0.457517876 -0.254103656 -0.222418686 0.120548916 0.442410424
[11] -0.489244128 -0.515799736 0.721977568 -0.505664504 2.496322940
[16] 1.750225707 0.984520682 -2.100076885 1.163387497 -1.847169628
[21] 1.026436385 0.037440380 1.144774125 0.388064700 0.887054154
[26] -2.255001857 1.226944467 1.003208672 0.076743724 -0.993589240
[31] 0.206843156 0.574956463 -0.598022350 -0.833522512 -1.080017806
[36] 0.135214303 -1.825708769 -1.780628015 0.247265491 -0.793415836
[41] 0.212738500 1.164304802 -0.725247172 0.243115883 -1.126207307
[46] -1.371712755 -0.192989989 0.526408617 -0.364194665 1.532130014
[51] 0.049059529 0.633819315 -1.828307686 -0.904938398 1.151212831
[56] 0.215133115 -0.005943572 0.174063562 1.388572216 0.885246936
[61] -0.702429671 -1.020938502 -1.164518317 1.056945977 0.090154386
[66] -0.113779942 -0.581737709 -0.538072691 -1.005314618 0.232909098
[71] -0.821975620 -1.328041902 1.831466306 0.512899687 0.979936284
[76] 0.129554265 -1.058449586 -1.386207153 0.293260089 -0.075869123
[81] -0.937398702 1.166745478 -2.157117728 -0.532425400 -0.360002817
[86] 0.502290260 -0.889727111 0.330029839 1.303207446 1.490104852
[91] 0.652688454 -0.708869813 0.296584041 -0.779736626 -1.014264718
[96] -1.651060837 0.415987780 0.442288473 0.099920962 -0.658623004

このデータのヒストグラムを作って、標準正規分布の曲線を重ねると以下のようになります。

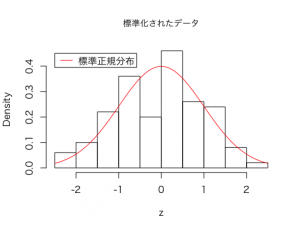
このように正規分布に従う確率変数は、そこから平均値を引いて標準偏差で割る、という変換をすることにより、標準正規分布に従う変数に加工することができます。

正規分布を標準化する利点

なぜ、わざわざ正規分布を標準化する必要があるのでしょうか？

理由は標準化してしまうことにより、確率変数のある実現値が得られた時、その値が分布の中でどれくらいの位置にあるのかが分かりやすくなるからです。

例

前述のように日本人成人男性の身長が平均値171、分散64の正規分布に従うとすると、ある人の身長が187cmだとします。

このままだと、この人の身長が全体の中でどれくらいの位置にあるのか一瞬ではわかりにくいですが、

$\displaystyle{\frac{187-171}{8}}=2.0$

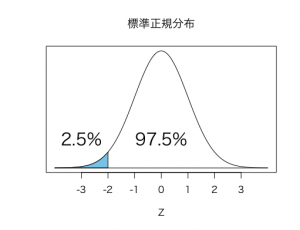
というように標準化してしまえば、68%-95%-99.7%の法則を利用して、すぐにこれが上位2.5%であると分かります。

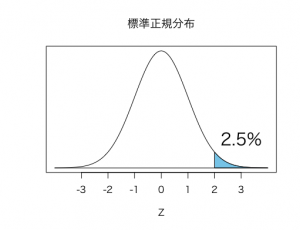
ちなみに、このように正規分布に従う確率変数Xを標準化して得られる確率変数Zの実現値zをZスコア（またはZ値）と呼びます。

Zスコアがわかるだけで、その観測された値が全体の上からどのくらいの位置にあるのか（または下からどのくらいの位置にあるのか）、が分かります。

そのため、統計学的仮説検定などにおいて、観測された値からZ値を求めて、検定の結論を出すということが行われます。
（統計検定に関しては「統計学の基礎」の中で詳しく解説します。）

練習問題

A君の通う高校では、ある統一テストの数学の点数が平均値μ=50点、分散σ²=25の正規分布に従うとします。またBさんの通う高校では、同じ統一テストの数学の点数が平均値μ=60点、分散σ²=49の正規分布に従うとします。

A君のこのテストの点数が40点、Bさんの点数が46点だったとすると、どちらの点数がそれぞれが通う高校の中で上位にランクされるでしょうか？

A君の高校

平均	分散	標準偏差	A君の点数
50	25	5	40

Bさんの高校

平均	分散	標準偏差	Bさんの点数
60	49	7	46

（１）この二人の点数のZスコアをそれぞれ求めて比較してください。
（２）この二人はそれぞれの高校で下から何％に位置しますか？

練習問題回答

（１）

•A君のZスコア
$z=\displaystyle{\frac{x-\mu}{\sigma}=\frac{40-50}{5}}=-2$

•BさんのZスコア
$z=\displaystyle{\frac{x-\mu}{\sigma}=\frac{46-60}{7}}=-2$

よって二人ともZスコア=-2なので、二人は各高校の中で同じ位置にいます。

（２）

以下の図のように、Zスコアが-2のとき、下から2.5%、上からは97.5%の位置になります。

MENU

標準正規分布とその確率密度関数、期待値、分散

正規分布の標準化

例

正規分布を標準化する利点

例

練習問題

練習問題回答

確率分布

スポンサー募集中。

更新・勉強会などの情報を受け取る。

理系の就職・職業訓練